
全程设计 第四章 指数函数、对数函数与幂函数 4.7数学建模活动:生长规律的描述
第四章 指数函数、对数函数与幂函数 4.7 数学建模活动:生长规律的描述

一 数学建模的过程 1.发现问题、提出问题; 2.分析问题、建立模型; 3确定参数、计算求解; 4.验证结果、改进模型
一、数学建模的过程 1.发现问题、提出问题; 2.分析问题、建立模型; 3.确定参数、计算求解; 4.验证结果、改进模型
二、建立函数模型解决实际问题 【典例1】四个变量y1y23y4随变量x变化的数据如下表: 10 15 20 25 30 2 26 101 226 401 626 901 2 32 1024 32768 1.05×106 3.36×107 1.07×109 3 2 10 20 30 40 50 60 2 4.322 5.322 5.907 6.322 6.644 6.907 则关于x呈指数型函数变化的变量是
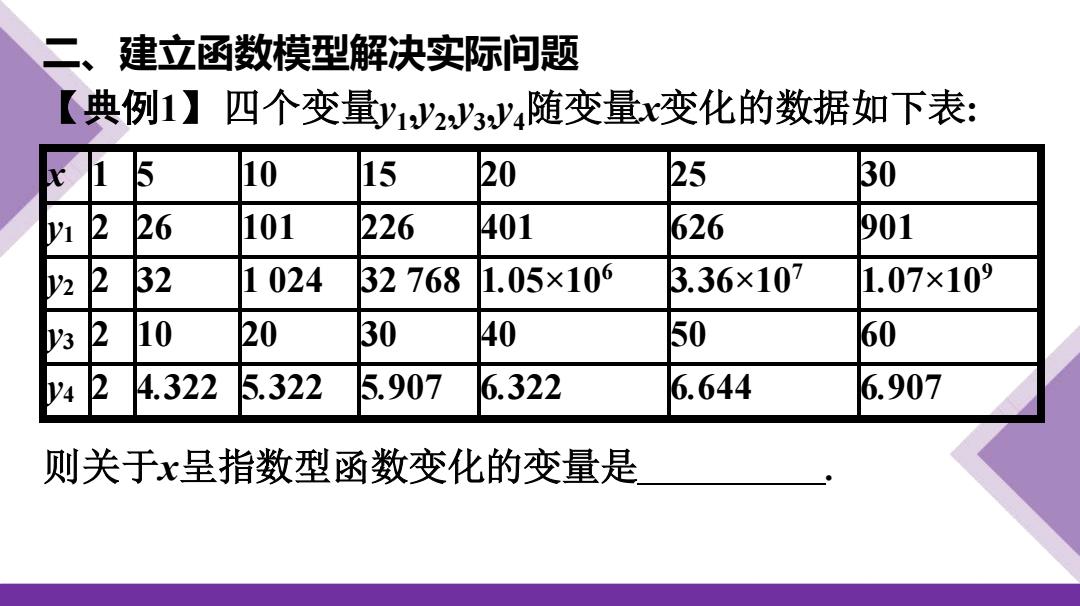
二、建立函数模型解决实际问题 【典例1】四个变量y1 ,y2 ,y3 ,y4随变量x变化的数据如下表: x 1 5 10 15 20 25 30 y1 2 26 101 226 401 626 901 y2 2 32 1 024 32 768 1.05×106 3.36×107 1.07×109 y3 2 10 20 30 40 50 60 y4 2 4.322 5.322 5.907 6.322 6.644 6.907 则关于x呈指数型函数变化的变量是

解析:指数型函数呈“爆炸式”增长,由所给表格知,四个变量 y12y3y4的值均是从2开始增长且越来越大,但是增长速度不 同,相比之下y2的增长速度最快,描出(化y2)的所有点,易知y2关 于x呈指数型函数变化 答案y2 反思感悟根据已知数据,选择适当函数.求解此类问题的关键 是弄清y随x的变化规律,考查了数据处理能力和直观想象能 力
解析:指数型函数呈“爆炸式”增长,由所给表格知,四个变量 y1 ,y2 ,y3 ,y4的值均是从2开始增长且越来越大,但是增长速度不 同,相比之下,y2的增长速度最快,描出(x,y2 )的所有点,易知y2关 于x呈指数型函数变化. 答案:y2 反思感悟 根据已知数据,选择适当函数.求解此类问题的关键 是弄清y随x的变化规律.考查了数据处理能力和直观想象能 力

【变式训练1】今有一组试验数据如下表所示,现准备用下列 函数中的一个模型来模拟这组数据满足的规律,其中最接近 试验数据的一个是( 2.0 3.0 4.0 5.1 6.0 1.5 4.04 7.5 12 18.01 2.1 A.y=log2t B.y= 2 cx-() D.y=2t- 答案:B
【变式训练1】今有一组试验数据如下表所示,现准备用下列 函数中的一个模型来模拟这组数据满足的规律,其中最接近 试验数据的一个是( ) t 2.0 3.0 4.0 5.1 6.0 y 1.5 4.04 7.5 12 18.01 A.y=log2t B.y= 𝒕 𝟐 -𝟏 𝟐 C.y= 𝟏 𝟐 𝒕 D.y=2t- 𝟓 𝟐 答案:B