新疆大学：《常微分方程》课程教学资源（授课教案）第五章 线性微分方程组

第五章线性微分方程组 在微分方程理论中，线性方程是非常重要的一部分。为了研究线性方程组方便，需要引进向量和矩阵 的记号，许多理论只有借助于线性代数的知识才可以作出适当和充分的解释。而本章的每一个结果的特殊 情形都可以对应高阶线性微分方程组的一个相应结果。 S5.1存在唯一性定理 5.1.1记号和定义 x'=a,(x+a2()x2+.+a(0xn+f() 考察形如： x2'=a()x+a2(x3+.+an(xn+() (5.1) x'=anu(x+an2()）x2+.+am()x。+n() 的一阶线性方程组，其中已知函数a,(d亿，j=12,.,n)和f()i=1,2,.,m在区间a≤t≤b上是连续 的，方程组(5.)关于x,x2,.,x及x,x',.,x是线性的。 我们引进下面的记号 a.(t)a2().an(t)Y 40aa0.4. (5.2) ani()a(0）.an() 这里A(0是nxn矩阵，它的元素是n2个函数a(),j=1,2,.,n f21 f() (5.3) 5( 这里f(),x,x'是n×1矩阵或n维列向量。借助于矩阵记号，方程组(5.)就可以写成下面的形式 x'=A()x+f((5.4) 矩阵或向量在区间a≤1≤b上称为连续，如果它的每一个元素都是区间a≤1≤b上的连续函数。 第1页共16页

第 1 页 共 16 页 第五章 线性微分方程组 在微分方程理论中，线性方程是非常重要的一部分。为了研究线性方程组方便，需要引进向量和矩阵 的记号，许多理论只有借助于线性代数的知识才可以作出适当和充分的解释。而本章的每一个结果的特殊 情形都可以对应高阶线性微分方程组的一个相应结果。 §5. 1 存在唯一性定理 5．1．1 记号和定义 考察形如： ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 11 1 12 2 1 1 2 21 1 22 2 2 2 1 1 2 2 5.1 n n n n n n n nn n n x a t x a t x a t x f t x a t x a t x a t x f t x a t x a t x a t x f t   = + + + +    = + + + +      = + + + +  的一阶线性方程组，其中已知函数 a t i j n ij ( )( , 1,2, , = ) 和 f t i n i ( )( =1,2, , ) 在区间 a t b   上是连续 的，方程组 (5.1) 关于 1 2 , , , n x x x 及 1 2 , , , n x x x    是线性的。 我们引进下面的记号 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 11 12 1 21 22 2 1 2 5.2 n n n n nn a t a t a t a t a t a t A t a t a t a t       =       这 里 A t( ) 是 n n 矩 阵 ， 它 的 元 素 是 2 n 个函数 ( ), , 1,2, , ij a t i j n = ， ( ) ( ) ( ) ( ) ( ) 1 1 1 2 2 2 5.3 n n n f t x x f t x x f t x x f t x x                   = = =                           这里 f t x x ( ), ,  是 n1 矩阵或 n 维列向量。借助于矩阵记号，方程组 (5.1) 就可以写成下面的形式 x A t x f t  = + ( ) ( ) (5.4) 矩阵或向量在区间 a t b   上称为连续，如果它的每一个元素都是区间 a t b   上的连续函数

b(0b2().() 4( 一个n×n矩阵B( b(0bz(0.b2n()） 或一个n维列向量u()= 山，(在区间a≤t≤b b(0bn20.bn() 上可微，如果它的每一个元素都在区间a≤1≤b上可微，它们的导数分别由下式给出： 「6，(0，().() 40 B'()= b6()b6(I.b5n() () b(b2()）.b() ( 矩阵B()或者向量u()在区间a≤t≤b上可积的，如果每一个元素都在区间a≤t≤b上可积，它们的积 a,0t心b0t.fia.(0dh (Su(O)d 分为：心B()h= )db)d.a.) Lu()d= [uz(t)dt ∫ibu)dt b.(O)dh.∫ib()h a 定义1设A()是区间a≤t≤b上的连续n×n矩阵，f()是同一区间a≤1≤b上的连续n维向量，方程 组x=A()x+f间(5.4)在某区间a≤1≤Ba,]e[a,b)的解就是向量u(),它的导 数d(d在区间a≤1≤B上连续且满足，(d=A()u(+f(),a≤1≤B 定义2初值问题x=A()x+f(),x(亿)=n(5.5)的解就是方程组(5.4)在包含1，的区间a≤1≤B 上的解u(),使得u(6)=7 (-e 解：0)=e）1 -e-且e和-e处处有连铁导数。 可跳0-日)-日小00是m, 例2证明n阶线性微分方程的初值问恩 I+a间-9++a0x+ax=f066 x()=7,x(6)=.,()=n, 其中a(),a(),.,an(t),f()是区间a≤t≤b上的已知函数，6∈[a,b],h.,n是已知常数 第2页共16页

第 2 页 共 16 页 一个 n n 矩阵 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 11 12 1 21 22 2 1 2 n n n n nn b t b t b t b t b t b t B t b t b t b t       =       或一个 n 维列向量 ( ) ( ) ( ) ( ) 1 2 n u t u t u t u t       =         在区间 a t b   上可微，如果它的每一个元素都在区间 a t b   上可微， 它们的导数分别由下式给出： ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 11 12 1 21 22 2 1 2 n n n n nn b t b t b t b t b t b t B t b t b t b t              =          ， ( ) ( ) ( ) ( ) 1 2 n u t u t u t u t          =          矩阵 B t( ) 或者向量 u t( ) 在区间 a t b   上可积的，如果每一个元素都在区间 a t b   上可积，它们的积 分为： ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 11 12 1 21 22 2 1 2 b b b n a a a b b b b n a a a a b b b n n nn a a a b t dt b t dt b t dt b t dt b t dt b t dt B t dt b t dt b t dt b t dt         =                   ， ( ) ( ) ( ) ( ) 1 2 b a b b a a b n a u t dt u t dt u t dt u t dt         =               定义 1 设 A t( ) 是区间 a t b   上的连续 n n 矩阵， f t( ) 是同一区间 a t b   上的连续 n 维向量，方程 组 x A t x f t  = + ( ) ( ) (5.4) 在某区间        t a b ( , ,   ) 的解就是向量 u t( ) ，它的导 数 u t ( ) 在区间    t 上连续且满足， u t A t u t f t t ( ) = +   ( ) ( ) ( ),  定义 2 初值问题 x A t x f t x t  = + = ( ) ( ), 5.5 ( 0 )  ( ) 的解就是方程组 (5.4) 在包含 0 t 的区间    t 上的解 u t( ) ，使得 u t( 0 ) = 例 1．验证向量 ( ) t t e u t e − −   =       − 是初值问题 ( ) 0 1 1 0 1 0 1 x x      = =         − 在区间 −   + t 上的解。 解： ( ) 0 0 1 0 1 e u e − −     = =       −   −   ，且 t e − 和 t e − − 处处有连续导数， 可以得到， ( ) ( ) 0 1 0 1 1 0 1 0 t t t t e e u t u t e e − − − −   −        = = =                 −   ，u t( ) 是给定初值问题的解。 例 2 证明 n 阶线性微分方程的初值问题 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 0 1 0 2 0 5.6 , , , n n n n n n x a t x a t x a t x f t x t x t x t    − − −  + + + + =     = = =   其中 a t a t a t f t 1 2 ( ), , , , ( ) n ( ) ( ) 是区间 a t b   上的已知函数， 0 1 2  , , , ,  n t a b     是已知常数

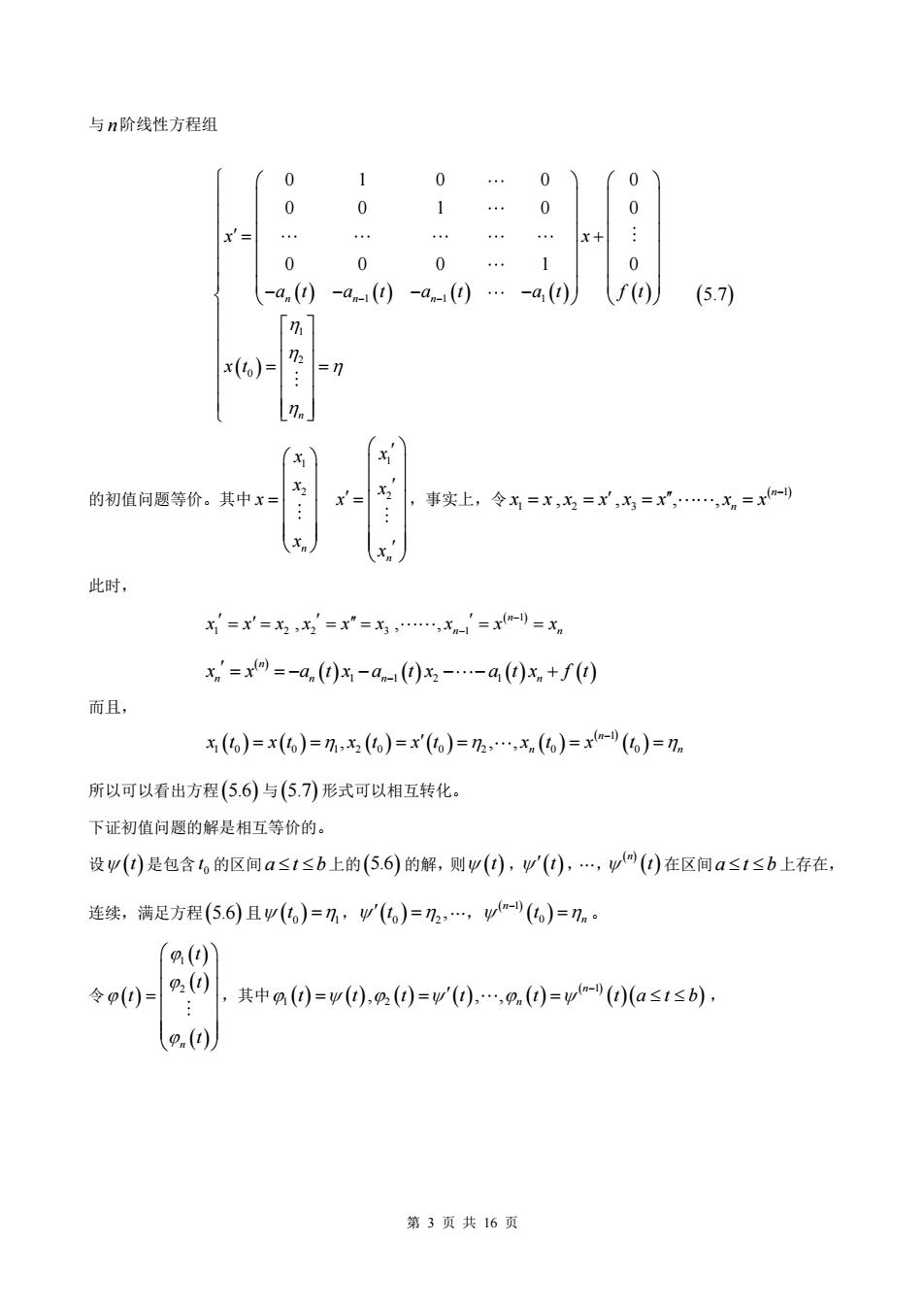
与n阶线性方程组 0 01 0 y 0 0 .1 -an(0-an-()-an(0.-a()） f( (5.7) x()= =n n 的初值问题等价。其中x= x= x 事实上，令x=x,为=x,=x,Xn=x x x. 此时， ==2=x”=.,xn=x=x x'=x=-a()x-an(0-a(0x+f) 而且， x（)=x()=n,x(6)=x（()=h2,.,x(o）=-(6)=n. 所以可以看出方程(5.6)与(5.7)形式可以相互转化。 下证初值问题的解是相互等价的。 设w()是包含6的区间a≤1≤b上的(5.6)的解，则y(0,W(),网)在区间a≤1≤b上存在， 连续，满足方程(5.6)且w(化)=7，(G)=n2,.,-()=n.。 g() 令p(0)= %() 其中A(0=(0),g(0)=w(),.,9()=w-()(a≤1≤b), 第3页共16页

第 3 页 共 16 页 与 n 阶线性方程组 ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 ( ) 1 2 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 n n n 5.7 n x x a t a t a t a t f t x t     − −              = +    − − − −             = =               的初值问题等价。其中 1 1 2 2 n n x x x x x x x x             = =                   ，事实上，令 ( 1) 1 2 3 , , , , n n x x x x x x x x − = = = =   此时， ( 1) 1 2 2 3 1 , , , n n n x x x x x x x x x − −    = = = = = =   ( ) ( ) 1 1 2 1 ( ) ( ) ( ) n n n n n x x a t x a t x a t x f t −  = = − − − − + 而且， ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 0 0 1 2 0 0 2 0 0 , , , n n n x t x t x t x t x t x t    − = = = = = =  所以可以看出方程 (5.6) 与 (5.7) 形式可以相互转化。 下证初值问题的解是相互等价的。 设  (t) 是包含 0 t 的区间 a t b   上的 (5.6) 的解，则  (t) ，(t)，.， ( ) ( ) n  t 在区间 a t b   上存在， 连续，满足方程 (5.6) 且   (t 0 1 ) = ，  (t 0 2 ) = ,.， ( ) ( ) 1 0 n n   t − = 。 令 ( ) ( ) ( ) ( ) 1 2 n t t t t           =         ，其中 ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) 1 1 2 , , , n n       t t t t t t a t b − = = =   

g' ) 9,() v() p() 显然满足p(6)=,且'() '() wa-(） p.( () -a0)a-(0-a.0w)+f 92(t） 9(） -an()g()-a(t)p()+f() (0 标明向量p(是(5.7)的解 0 1 0 0 g()】 0 0 %() 0 0 1 p-( 0 -an(d-an-().-a,(t)-a()八p.()ft) 4() 反之，假设向量u(是在包含。的区间a≤1≤b上是(5.7)的解，u()= 4(t) ,并定义函数 4.(0 o(t)=4,(),由(5.7)的第一个方程，我们得到o(t)=4'(t)=山2(t),由第二个方程得到 o(t)=山'()=4()，由第n-1个方程得到o-()=-(①=山()，由第n个方程得到： o()=4,'()=-a()4()-an()42()-a()4n()-a)）4.()+f) =-a,()o-()-4,0)o-()-a.()o(0+f) 由此即得：o()+a()o-()+a2()o-()+.+an(0o()=f() 同时得到，o()=4()=,0-()=4()=.,这就说明o()是(5.6)的一个解。 由上面的讨论可以知道，(5.6)的初值问题与(5.)的初值问题在下列意义下等价：给定其中的一个初值问 题的解，就可以构造另一个初值问题的解。注意的是，每一个阶线性微分方程可以化为n个一阶线性微 分方程构成的方程组，反之却不成立如方程角：文0上行x侧 就不能化为一个二阶微分方程。 S5.1.2存在唯一性定理 教学目的：掌握线性方程组的存在唯一性定理 第4页共16页

第 4 页 共 16 页 显然满足   (t 0 ) = ，且 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 1 3 2 1 1 1 n n n n n n t t t t t t t t t t t a t t a t t f t              − −                            = = =                        − − − +     ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 3 1 1 1 2 1 1 2 1 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 n n n n n n n t t t a t t a t t f t t t t a t a t a t a t f t t          − −     = − − − +                 = +       − − − −         标明向量  (t) 是 (5.7) 的解。 反之，假设向量 u t( ) 是在包含 0 t 的区间 a t b   上是 (5.7) 的解， ( ) ( ) ( ) ( ) 1 2 n u t u t u t u t       =         ，并定义函数 (t u t ) = 1 ( ) ，由 (5.7) 的第一个方程，我们得到  (t u t u t ) 1 2 ( ) ( )   = = ，由第二个方程得到  (t u t u t ) 2 3 ( ) ( ),   = = ，由第 n−1 个方程得到 ( ) ( ) ( ) ( ) 1 1 n n n  t u t u t − − = =  ，由第 n 个方程得到： ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 2 1 1 1 2 1 2 n n n n n n n n n t u t a t u t a t u t a t u t a t u t f t a t t a t t a t t f t     − − − − = = − − − − − +  = − − − − + 由此即得： ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 n n n n     t a t t a t t a t t f t − − + + + + = 同时得到，   (t u t 0 1 0 1 ) = = ( ) ， ， ( ) ( ) ( ) 1 0 0 n n n   t u t − = = ，这就说明  (t) 是 (5.6) 的一个解。 由上面的讨论可以知道， (5.6) 的初值问题与 (5.7) 的初值问题在下列意义下等价：给定其中的一个初值问 题的解，就可以构造另一个初值问题的解。注意的是，每一个 n 阶线性微分方程可以化为 n 个一阶线性微 分方程构成的方程组，反之却不成立。如方程组： 1 2 1 0 0 1 x x x x x      = =         就不能化为一个二阶微分方程。 §5．1．2 存在唯一性定理 教学目的：掌握线性方程组的存在唯一性定理

本节研究初值问题：x=A()x+∫()，x(。)=7(5.S)的解的存在唯一性定理，为了采用逐步逼近法 证明该定理，先引入一些相关概念 1.范数 对于n×n矩阵A=(a,)和n维向量 定义意数为川-之a-2 矩阵或向量的范数具有下面两个性质： (1)A≤4B,A≤A4:(2)A+≤A+B,kx+≤+ 2.收敛性 向量序列{x}, 称为收敛的，如果对每一个i(i=1,2,.,)数列都是收敛的。 x() 向量函数序列{x()},x() x2() 称为在区间a≤1≤b上收敛的（一致收敛的），如果对每一个 (xt(0) i(=1,2,.,n)函数序列{x4()}在区间a≤1≤b是收敛的（一致收敛的）。区间a≤1≤b一致收敛的连 续函数序列{x,()}的极限向量函数仍是连续的。 注：①维氏判别法对于向量函数级数也是成立，即，如果()训sM,a≤1≤b,级数∑M是收 敛的，则∑x()在区间a≤1≤b是一致收敛的。 ②积分号下取极限的定理对于向量函数也成立，即如果连续向量函数序列{x()}在区间a≤1≤b是一致 收敛的，则im心x)dt-心m()d山 ③上述所谈到的定义和结果，对于一般的矩阵函数序列仍然成立。 定理1（存在唯一性定理）如果A(t)是n×n矩阵，f()是n维列向量，它们都在区间a≤t≤b上连续， 第5页共16页

第 5 页 共 16 页 本节研究初值问题： x A t x f t x t  = + = ( ) ( ), 5.5 ( 0 )  ( ) 的解的存在唯一性定理，为了采用逐步逼近法 证明该定理，先引入一些相关概念。 1．范数 对于 n n 矩阵 ( ij)n n A a  = 和 n 维向量 1 2 n x x x x       =       ，定义范数为： , 1 n ij i j A a = =  ， , 1 n i i j x x = =  矩阵或向量的范数具有下面两个性质： （1） A B A B    ， Ax A x   ；（2） A B A B +  + ， x y x y +  + 2．收敛性 向量序列   1 2 , k k k k nk x x x x x       =         称为收敛的，如果对每一个 i i n ( =1,2, , ) 数列都是收敛的。 向量函数序列  ( ) ( ) ( ) ( ) ( ) 1 2 , k k k k nk x t x t x t x t x t       =         称为在区间 a t b   上收敛的（一致收敛的），如果对每一个 i i n ( =1,2, , ) 函数序列 x t ik ( ) 在区间 a t b   是收敛的（一致收敛的）。区间 a t b   一致收敛的连 续函数序列 x t k ( ) 的极限向量函数仍是连续的。 注：① 维氏判别法对于向量函数级数也是成立，即，如果 ( ) , k k x t M a t b    ，级数 1 k k M  =  是收 敛的，则 ( ) 1 k k x t  =  在区间 a t b   是一致收敛的。 ② 积分号下取极限的定理对于向量函数也成立，即如果连续向量函数序列 x t k ( ) 在区间 a t b   是一致 收敛的，则 lim lim ( ) ( ) b b k k x x a a x t dt x t dt → → =   ③上述所谈到的定义和结果，对于一般的矩阵函数序列仍然成立。 定理 1 （存在唯一性定理）如果 A t( ) 是 n n 矩阵， f t( ) 是 n 维列向量，它们都在区间 a t b   上连续