《线性代数》课程教学课件（PPT讲稿，C）第四章 线性方程组 4-2 齐次线性方程组

第四章线性方程组 由性质4.2.1、4.2.2知，齐次线性方程组(4-5) 的解向量的线性组合仍是(45)的解向量.即 设5,52，5n,都是(4-5)的解向量，2,22，.n， 是为任意数，则 151+九252+.+九m-5m-r 仍是(4-5)的解。 方程组(4-5)的全部解向量构成个一个向量空间， 称为方程组(4-5)的解空间

第四章 线性方程组 由性质4.2.1、4.2.2知，齐次线性方程组(4-5) 的解向量的线性组合仍是(4-5)的解向量 . 即 设 都是(4-5)的解向量， 是为任意数，则     nr , , , 1 2    nr , , 1 2 1 1  2 2  nr nr 仍是(4-5)的解. 方程组(4-5)的全部解向量构成个一个向量空间， 称为方程组(4-5)的解空间

第四章线性方程组 方程组4-5)的全部解向量构成个一个向量空间， 称为方程组4-5)的解空间.它是R”的一个子空间. 如果方程组(4-5)有非零解，由性质4.2.1、 4.2.2知，它一定有无穷多非零解.要求出(4-5)的 所有解，只需求出解空间的一组基就行了. 下面我们来介绍求解空间的一组基 设线性方程组(4-5)系数矩阵A的秩为r,即 R(A)=r不妨假设A的前个列向量线性无关，则A 的行最简形为

第四章 线性方程组 方程组(4-5)的全部解向量构成个一个向量空间, 称为方程组(4-5)的解空间. 它是R n的一个子空间. 如果方程组(4-5)有非零解，由性质4.2.1、 4.2.2知，它一定有无穷多非零解.要求出(4-5)的 所有解，只需求出解空间的一组基就行了. 下面我们来介绍求解空间的一组基 设线性方程组(4-5)系数矩阵A的秩为r, 即 R(A)=r. 不妨假设A的前r个列向量线性无关, 则A 的行最简形为

第四章线性方程组 P+1 0 1 b 6n 0 0 0 。 0 0 0 0 0 与I对应的线性方程组为 =-b+1X,+1-.-b1,nXm (4-7) X,=-b,+1X,+1-.-bmXa 线性方程组(4-7)与(4-5)同解

第四章 线性方程组 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 r n rr rn b b b b I                                1 1, 1 1 1, , 1 1 , (4 7) r r n n r r r r r n n x b x b x x b x b x                   与 I 对应的线性方程组为 线性方程组(4-7)与(4-5)同解

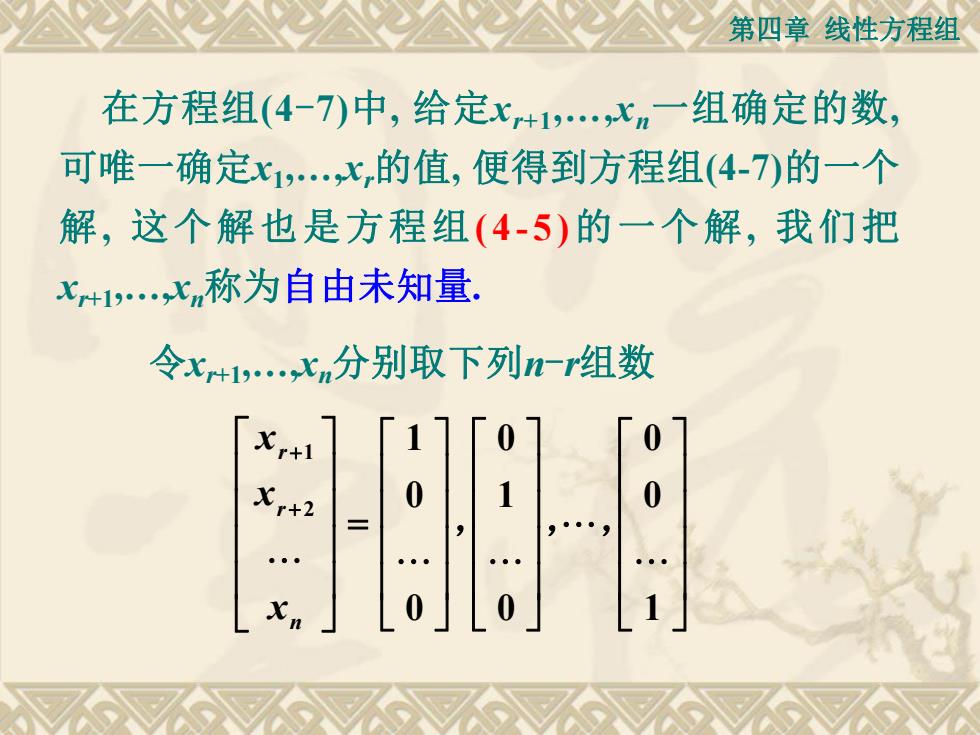
第四章线性方程组 在方程组(4-7)中，给定x+1,比m一组确定的数 可唯一确定x1，·x,的值，便得到方程组(4-7的一个 解，这个解也是方程组(4-5)的一个解，我们把 X+1心n称为自由未知量。 令x+iXn分别取下列n-r组数 0 X+2 0 0

第四章 线性方程组 在方程组(4-7)中, 给定xr+1 ,.,xn一组确定的数, 可唯一确定x1 ,.,xr的值, 便得到方程组(4-7)的一个 解, 这个解也是方程组(4 -5 )的一个解, 我们把 xr+1 ,.,xn称为自由未知量. 令xr+1 ,.,xn分别取下列n-r组数 1 2 1 0 0 0 1 0 0 0 1 r r n x x x                                                  ， ，

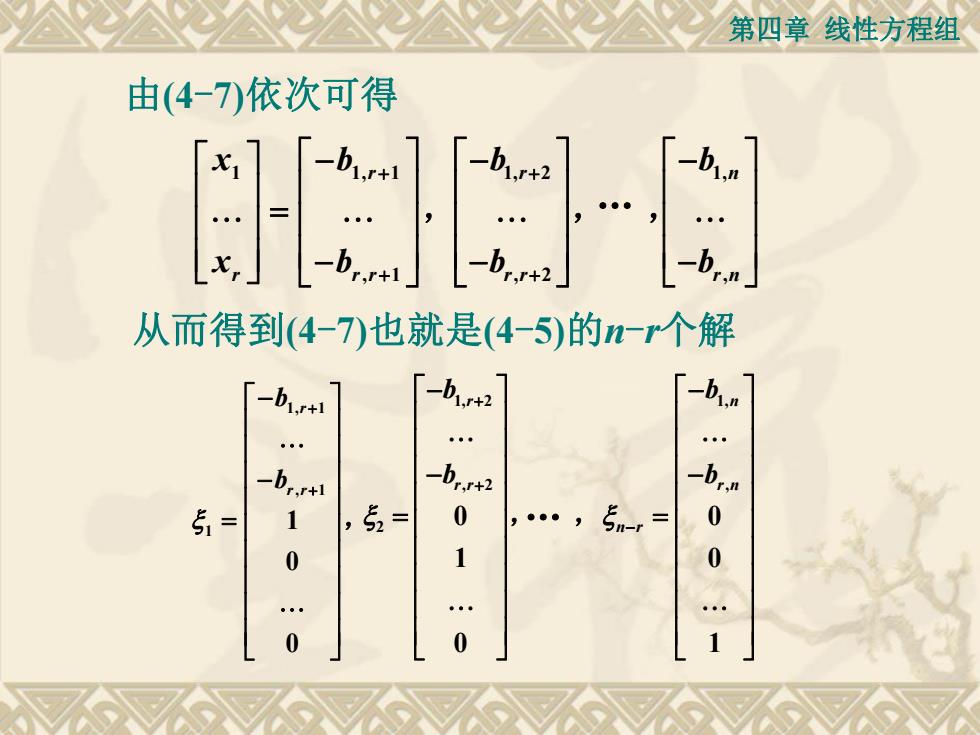
第四章线性方程组 由(4-7)依次可得 -b1r+1 从而得到(4-7)也就是(4-5)的n-r个解 b1.r+1 -b1+2 -bi.n . . b.r -br2 51= 1 52= 0 5m-,= 0 0 1 0 0 0

第四章 线性方程组 1 1, 1 , 1 r r r r x b x b                    ， 1, 2 , 2 r r r b b          ， 1, , n r n b b        ， 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解 1, 1 , 1 1 1 0 0 r r r b b              ， 1, 2 , 2 2 0 1 0 r r r b b              ， 1, , 0 0 1 n r n n r b b             .