《线性代数》课程学习指导（C）第四章 线性方程组_典型例题

第四章线性方程组 典型例题 例4-1设A,B都是n阶方阵，如果AB=0,试证明4)+R(B)≤n 证明因为AB=0,故B的每个列向量b,(=1,2,.,川都是4=0的解向 量。如果R(4)=r,则A(=0有n-r个线性无关的解向量，而b,b2,.,bn中线 性无关的有R(B)个，故R(B)≤n-r=n-Rd),即R(A)+RB)≤n. 例42设非齐次线性方程组4=6的系数矩阵的秩为工，万，办，万n是它 的n-r+1个线性无关解，试证它的任一解可表示为x=k元+k+.+k7, 其中k+k2+.+kr=1. 证明由线性方程组的性质可知 元-in-r41,i2-7nrl,.,inr-in-r4l (1) 是=0的解，因为R)=r,所以A=0的基础解系所含向量的个数为n-x 以下证明(1)线性无关。 设有，2，r,使得 1(7,-刃ni）+(n2-nn-ri)++元n-(7nr-nnri)=0 即 名i+i++i-(+++九)nnm=d 由元，2，.，im-1线性无关，故元=入2=.=元n,=-(亿+元2+.+元n)=0,从而 元-in-r1,i2-7nr1,.,in-r-inrl 线性无关.再由4A=b的结构定理，可知 x=k(⑦-in)+k,(⑦2-i-H)+.kn-(⑦-ir)+1-r4 =ki+ki2+.+kn47n-rl 其中，k+k2+.+knH=1

第四章 线性方程组 典型例题 例 4-1 设 A, B 都是 n 阶方阵，如果 A B =0 ，试证明 RA RB  n 证明 因为 A B =0,故 B 的每个列向量 b i n i 1,2,  , 都是 0   Ax  的解向 量。如果 RA  r ，则 0   Ax  有 n  r 个线性无关的解向量，而 b b bn , , , 1 2  中线 性无关的有 RB 个，故 RB  n  r  n  RA ，即 RA RB  n . 例 4-2 设非齐次线性方程组 Ax b    的系数矩阵的秩为 r,   n     , , , 1 2 是它 的n-r+1个线性无关解，试证它的任一解可表示为  1 1  2 2   nr1 nr1 x k  k  k       , 其中 k1  k2  knr1 1. 证明 由线性方程组的性质可知 1 1 2 1 1 , , ,  nr  nr nr nr        （1） 是 0   Ax  的解，因为 RA  r ,所以 0   Ax  的基础解系所含向量的个数为 n-r， 以下证明(1)线性无关。 设有   nr , , , 1 2  ，使得                (  )  (  )   (  )  0 1 1  n r 1 2  2  n r 1  n r  n r  n r 1 即               (  . )  0 11 2  2  n r  n r 1 2 n r  n r 1 由 1 2 1 , , ,   nr     线性无关，故 1  2  nr  (1  2 . nr )  0,从而 1 1 2 1 1 , , ,  nr  nr nr nr        线性无关.再由 Ax b    的结构定理，可知 1 1 1 2 2 1 1 1 ( ) ( ) ( )               n r   n r  n r n r  n r  n r x k   k   k            1 1  2 2   nr1 nr1 k  k  k      其中, k1  k2  knr1 1

例43试求下列方程组有解的充要条件 [x1-x2=a1 x-x3 =az Xn-1-X=da-l -x+x =a 解对方程组的增广矩阵施行初等行变换 [1-10.00411 -10.00a 01-1.00a2 0 1 -1 .00a2 001.00a 00 .00a A= → 0001-1a 0 00 .1-1a -100.01a.」 00 0 -004 虽然。利=-小.因此只有当交时风=-1此时方程组才 有解，即上过方程组有解的充要条件是∑a,=0. 例44求解下列方程组 +x2-3x3-x4=1 3x1-x2-3x3+4x4=4 x+5x3-9x3-8x4=0 解对方程组的增广矩阵施行初等变换 [11-3-11-11-3-111 A=3-1-344 15-9-805-04-6-7-100000 333 1-3-] 10月5， 于是有

例 4-3 试求下列方程组有解的充要条件                     n n n n n x x a x x a x x a x x a 1 1 1 1 3 2 1 2 1 . 解 对方程组的增广矩阵施行初等行变换 A=                           n n a a a a a 1 0 0 . 0 1 0 0 0 . 1 1 . . . . . . . 0 0 1 . 0 0 0 1 1 . 0 0 1 1 0 . 0 0 1 3 2 1                            n i i n a a a a a 1 1 3 2 1 0 0 0 . 0 0 0 0 0 . 1 1 . . . . . . . 0 0 1 . 0 0 0 1 1 . 0 0 1 1 0 . 0 0 虽然， R(A)  n 1 ，因此，只有当  n i i a 1 =0 时 ( ) 1 _ R A  n  此时方程组才 有解，即上过方程组有解的充要条件是  n i i a 1 =0. 例 4-4 求解下列方程组                  5 9 8 0 3 3 4 4 3 1 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 解 对方程组的增广矩阵施行初等变换                                                    0 0 0 0 0 0 4 6 7 1 1 1 3 1 1 0 4 6 7 1 0 4 6 7 1 1 1 3 1 1 1 5 9 8 0 3 1 3 4 4 1 1 3 1 1 3 2 2 1 3 1 _ 3 r r r r r r A                                                 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 1 1 3 1 1 1 4 7 4 3 2 5 4 3 4 3 2 1 4 7 4 3 2 ( ) 1 2 1 4 2 r r r 于是有

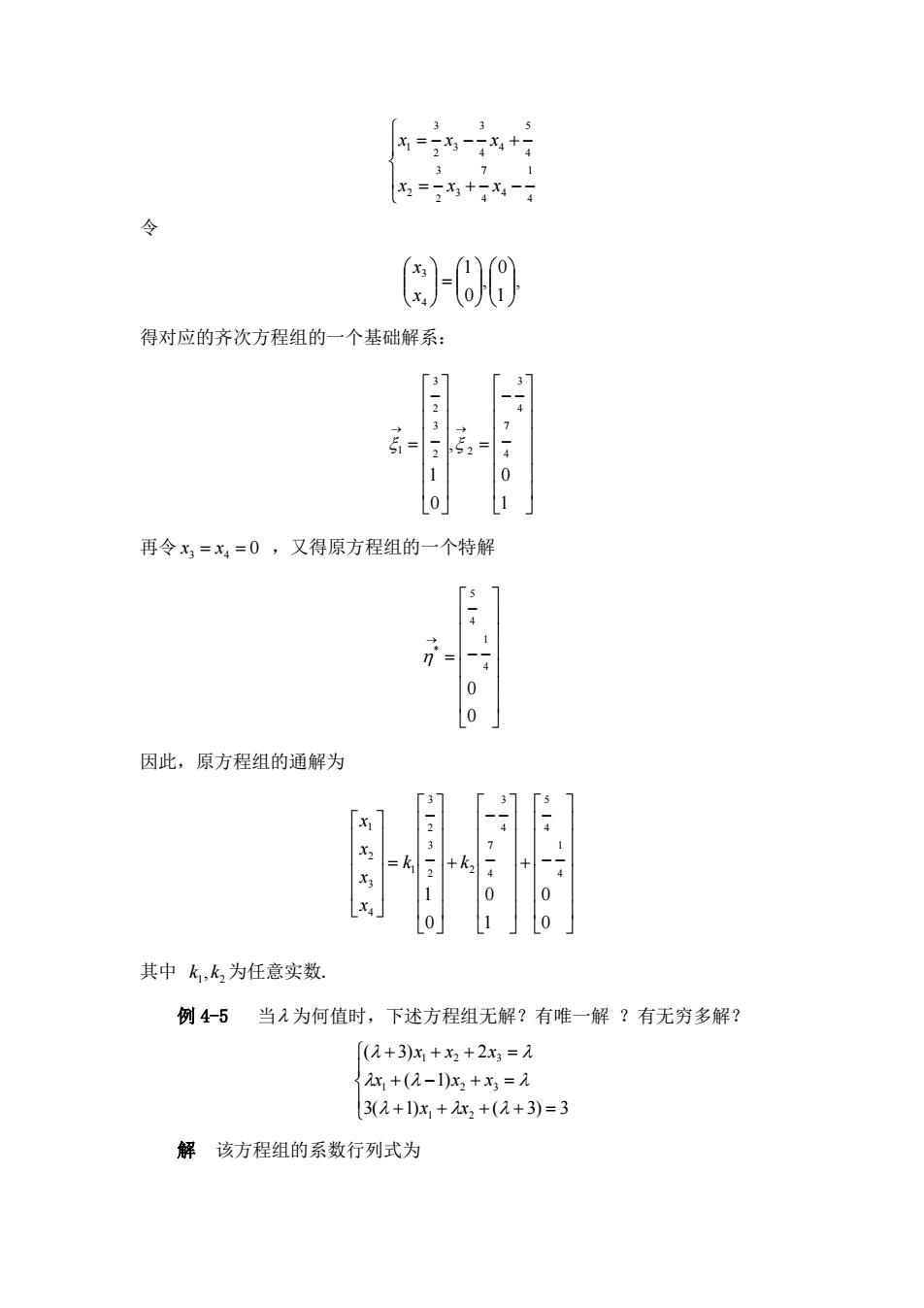
X=53-:x4+ =:+- 令 &-60 得对应的齐次方程组的一个基础解系： 再令x=x=0，又得原方程组的一个特解 0 因此，原方程组的通解为 + 0 o1」0J 其中k,k为任意实数 例4-5当为何值时，下述方程组无解？有唯一解？有无穷多解？ (元+3)x+x2+2x3=元 {x+(-1)x2+x3=元 3(2+)x,+x2+(2+3)=3 解该方程组的系数行列式为

                 1 4 4 7 4 3 3 2 2 5 4 4 3 4 3 3 2 1 x x x x x x 令 , 1 0 , 0 1 4 3                         x x 得对应的齐次方程组的一个基础解系：                                          1 0 , 0 1 7 4 3 4 2 3 2 3 2  1  再令 x3  x4  0 ，又得原方程组的一个特解                      0 0 1 4 5 4 *  因此，原方程组的通解为                                                                        0 0 1 0 0 1 1 4 5 4 7 4 3 4 2 3 2 3 2 1 4 3 2 1 k k x x x x 其中 1 2 k , k 为任意实数. 例 4-5 当  为何值时，下述方程组无解？有唯一解 ？有无穷多解？                   3( 1) ( 3) 3 ( 1) ( 3) 2 1 2 1 2 3 1 2 3         x x x x x x x x 解 该方程组的系数行列式为

1+312 D=22-11=(a-1) 3(元+1)元2+3 显然当≠0且2≠1时，D≠0，此时系数矩阵A与增广矩阵A的秩相同， 都等于未知数的个数，方程组有唯一解. 当入=0时，原方程组的增广矩阵为 「3120]「31201 [3120 A=0-1105→0-1105→0-110 30330-1130003 故R(A)=2,R(A)=3方程组无解. 当入=1时，原方程组的增广矩阵为 「41211「41211「4121] A=10111011-21011 614320220000 于是R()=R()=2<3,从而方程组有无穷多解

D= ( 1) 3( 1) 3 1 1 3 1 2 2               显然当   0 且  1 时， D  0 ，此时系数矩阵 A 与增广矩阵 _ A 的秩相同， 都等于未知数的个数，方程组有唯一解. 当   0 时, 原方程组的增广矩阵为                                          0 0 0 3 0 1 1 0 3 1 2 0 0 1 1 3 0 1 1 0 3 1 2 0 3 0 3 3 0 1 1 0 3 1 2 0 3 1 3 2 _ r r r r A 故 R(A)  2, ( ) 3 _ R A  方程组无解. 当  1 时,原方程组的增广矩阵为                                     0 0 0 0 1 0 1 1 4 1 2 1 2 0 2 2 1 0 1 1 4 1 2 1 6 1 4 3 1 0 1 1 4 1 2 1 3 1 3 2 2 _ r r r r A , 于是 R(A)  ( ) 2 3 _ R A   ，从而方程组有无穷多解