
6x - 4x2 = 24.243x, -2x2 =12,-2 :123x -2x2 = 12,-212①36xi - 4x2 = 24.-4 : 2462123x -2x2 = 12,-2①+Q0= 0.加油!
1 2 1 2 6 4 24. 3 2 12, x x x x 3 2 12 6 4 24 1 2 1 2 3 2 12, 6 4 24. x x x x 6 4 24 3 2 12 3 2 12, 1 2 0 0. x x 3 2 12 0 0 0 1 2 -2 1 + 2

在上述变换过程中,用到下面的三种形式的变换(1) 交换两个方程的位置(2)用非0 的数乘以某一个方程;(3)某一个方程乘以常数k后加到另一个方程上去我们把以上三种变换叫做线性方程组的初等变换高斯消元法解线性方程组就是用初等变换来化简方程组由于三种变换都是可逆的,所以变换前的方程组与变换后的方程组是同解的。加油!
(1)交换两个方程的位置; (2)用非0的数乘以某一个方程; (3)某一个方程乘以常数k后加到另一个方程上去 我们把以上三种变换叫做线性方程组的初等变换. 高斯消元法解线性方程组就是用初等变换来 化简方程组. 在上述变换过程中,用到下面的三种形式的变换 由于三种变换都是可逆的,所以变换前的 方程组与变换后的方程组是同解的.

二、矩阵的初等变换1.定义下面三种变换称为矩阵的初等行变换:(1)对调两行(对调i,j两行,记作r,r);(2)以数 k≠0 乘以某一行的所有元素;(第i行乘k,记作r×k)(3)把某一行所有元素的k倍加到另一行对应的元素上去(第i行的k倍加到第i行上记作r;+kr,)加油!
1.定义 下面三种变换称为矩阵的初等行变换: 1 , , i j 对调两行(对调i j r r 两行 记作 ); 2 0 ; , i k i k r k 以数 乘以某一行的所有元素 (第 行乘 记作 ) 3 . i j k j k i r kr 把某一行所有元素的 倍加到另一行 对应的元素上去(第 行的 倍加到第 行上 记作 ) 二、矩阵的初等变换

2.同样可定义矩阵的初等列变换(所用记号是把“r"换成“c"),包括如下的三种变换。(1)对调矩阵中的两列。(2)以非零常数k乘以矩阵某一列的全部元素。(3)把矩阵中某一列全部元素的k倍加到另外一列的对应元素上3.矩阵的初等行变换与初等列变换统称为初等变换加油!
3. 矩阵的初等行变换与初等列变换统称为初等变换. 2. 同样可定义矩阵的初等列变换(所用记号是 把“r”换成“c”),包括如下的三种变换。 (1)对调矩阵中的两列。 (2)以非零常数k乘以矩阵某一列的全部元素。 . (3) 一列的对应元素上 把矩阵中某一列全部元素 的k倍加到另外
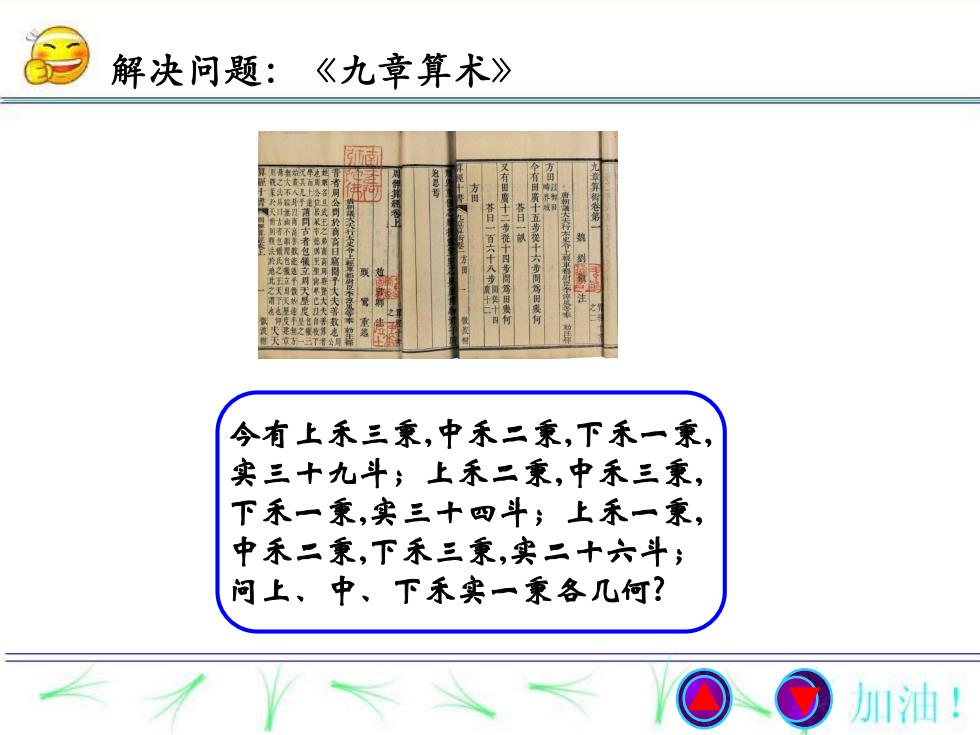
解决问题:《九章算术》今有上禾三秉,中禾二东,下禾一秉实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉中禾二秉,下禾三秉,实二十六斗问上、中、下禾实一秉各几何?加油!
今有上禾三秉,中禾二秉,下禾一秉, 实三十九斗;上禾二秉,中禾三秉, 下禾一秉,实三十四斗;上禾一秉, 中禾二秉,下禾三秉,实二十六斗; 问上、中、下禾实一秉各几何? 解决问题:《九章算术》