
第四章S3n维向量空间的正交性一、内积的定义及性质二、向量的长度及性质三、n维向量的正交性四、施密特正交化方法加油!
§3 n维向量空间的正交性 第四章 一、内积的定义及性质 二、向量的长度及性质 三、n维向量的正交性 四、施密特正交化方法
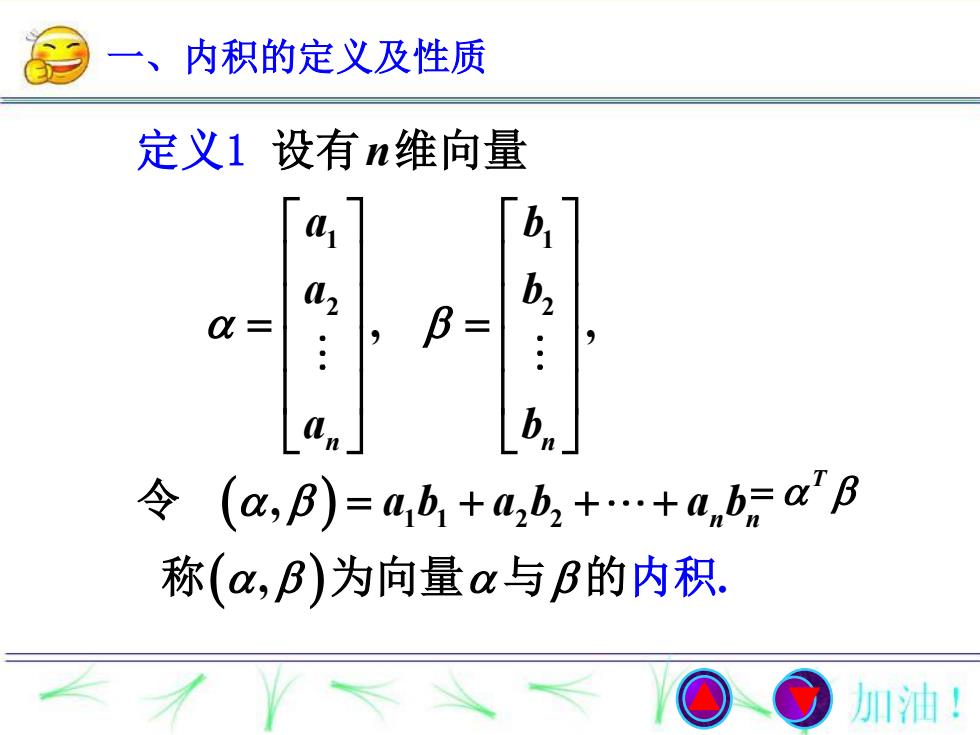
一、内积的定义及性质定义1设有n维向量Dab,a2α =b令 (α,β)=ab, +a,b, +...+a,b=α"β11称(α,β)为向量α与β的内积.加油!
1 1 2 2 1 1 2 2 , , , , . n n n n n a b a b a b a b a b a b 设有 维向量 令 称 为向量 与 定 1 的内积 义 一、内积的定义及性质 T

内积的运算性质(其中α,β,为n维向量,k为实数):(1)(α,α)≥0,且当α 0时有(α,α)>0(2)(α,β) =(β,α);(3)(kα,β) = k(α,β);(4)(α+β,)=(α,)+(β,),加油!
内积的运算性质 其中 , , , : 为n k 维向量 为实数 (2) , , ; (3) , , ; k k (4) , , , . (1) , 0, 0 , 0; 且当 时有

二、向量的长度及性质定义2(α,α) = ya +a +...+a称为向量α的长度(或范数),记作α向量的长度具有下述性质:1.非负性 当α±0时,α>0;当α=0时,α=0;2.齐次性 I/αl= [α;3.三角不等式α+β≤α+β加油!
定义2 2 2 2 1 2 , . n a a a 称为向量 的长度(或范数),记作 向量的长度具有下述性质: 1. 0 , 0; 0 , 0; 非负性 当 时 当 时 2. ; 齐次性 3. . 三角不等式 二、向量的长度及性质

若α=1,则称α为单位向量.如果α±0,由长度的概念得就是一个单位向量a1用非零数乘以向量α得到一个与α同方向的α单位向量,通常称为把向量α单位化加油!
若 1 , . 则 称 为 单 位 向 量 1 0, . 如 果 由 长 度 的 概 念 得 就 是 一 个 单 位 向 量 1 . 用非零数 乘以向量 得到一个与 同方向的 单位向量,通常称为把向量 单位化