
OOA第7章练习题、填空、选择题:1+n1.写出级数的前五项:台1+n?1112.级数!.-的一般项为u,=,部分和s,=+54525353.已知级数u,收敛于1,则级数u,收敛于台2n4.若级数u则u的部分和sn+1二5.级数>)u,的一般项u,趋于零,是该级数收敛的C1充分条件(B)必要条件(A)充分必要条件(D)既不充分、又非必要条件(C)
第7章练习题 1

OOA)6.级数u.的部分和数列S,存在极限,是该级数收敛的1-1(A)充分条件(B)必要条件(C)充分必要条件(D)既不充分、又非必要条件7.若级数u,收敛,)v发散,a为正常数,则级数(u,-v)=171=1=1一定收敛(B)一定发散(A)(C)收敛性与入有关(D)无法断定其敛散性K8.设k、g为非零常数,则级数)收敛的充分条件是-(A)1l<1(B)(g/≤1(C)[g|>1(D)la/≥17(9.下列级数收敛是oo01)43%ODMmn(+1)12Z(Vn+i-Vn)(B)(C)(D)(A)5"12nn=1u=1n=12
2
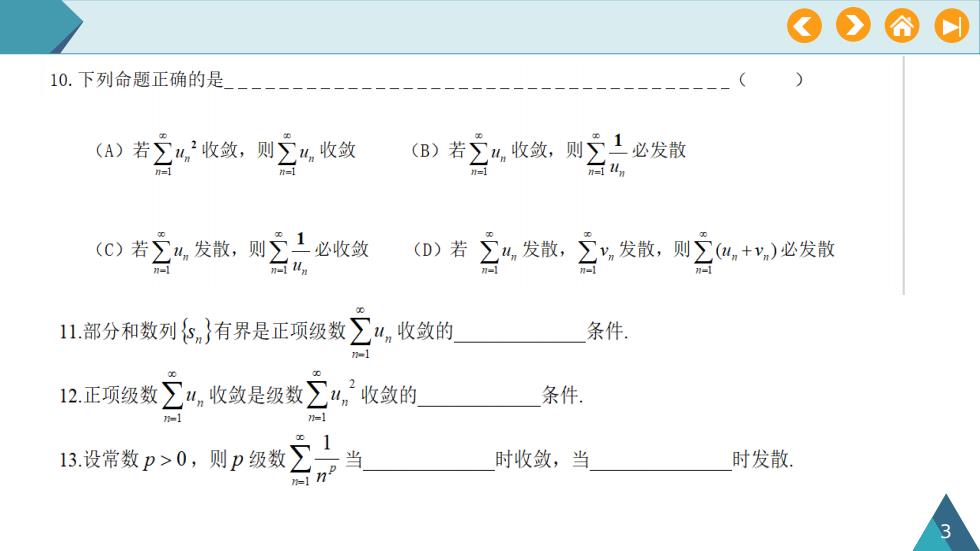
OOA210.下列命题正确的是(B)若u,收敛,则之必发散(A)若≥u收敛,则≥u,收敛unn=1n=1n=100(C)若u发散,则一必收敛Zun(D)若,发散,发散,则(u,+v,)必发散un--1n=la00u,收敛的条件11.部分和数列s.有界是正项级数n=180712.正项级数Zu,收敛是级数条件.2收敛的=1n=113.设常数P>0,则P级数之1当时收敛,当时发散.neinpT
3

AA条件.14.级数la|收敛,是级数之a.收敛的I1115.下列级数中,为绝对收敛级数的是(-1)"9n2(-1-2(-(B)(c)(D)(A)2n+1wn-in+1-1n-1n-1716.下列级数中,为条件收敛级数的是51Z(-1)-1 n2CZ(-1)"-1(c)(A)(B)Z(-1)1 /n(D)nJnn+1-1n-1n-1n-l17.交错级数-1)-2C绝对收敛的充分必要条件是np4l7-1(B)(D)(A)(c) p>1p>0P≥0p≥1Dk+n则级数之118.设常数k>0,!Ln2-1(B)发散条件收敛(c)(A)绝对收敛(D)敛散性与k有关一a1则级数19.设常数q>0,sinIn2n-1(B)(c)发散条件收敛(D)敛散性与α有关(A)绝对收敛/
4
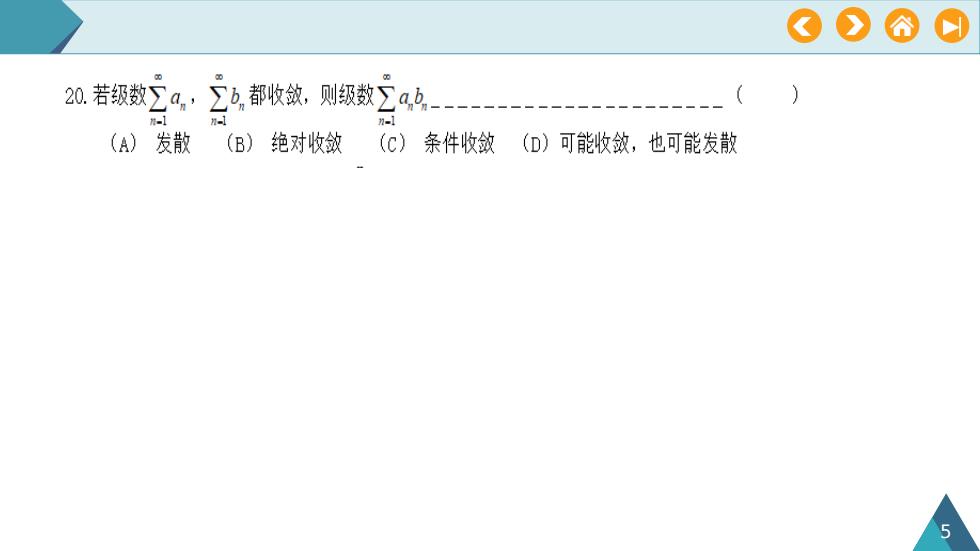
OAo0a2b.都收敛,则级数。20.若级数a,,Cab-1n-1n-1(A)发散(c)条件收敛(B)绝对收敛(D)可能收敏,也可能发散L
5