《线性代数》课程教学资源（课件讲稿，C）第二章 2-2向量及其线性运算

第二章矩阵与向量第二节向量及其线性运算

第二章 矩阵与向量 第二节 向量及其线性运算

第二章矩阵与向量3123x - 2x2 =12,+×2X22xi + x2 =1.2312(2, -3)21232(-3)2XX2

第二章 矩阵与向量        2 1. 3 2 12, 1 2 1 2 x x x x 3 2 12 2 1 1        1 x  2 x  1 2 3 2 12 2 1 1 x x                      2, 3    3 2 12 2 3 2 1 1                      

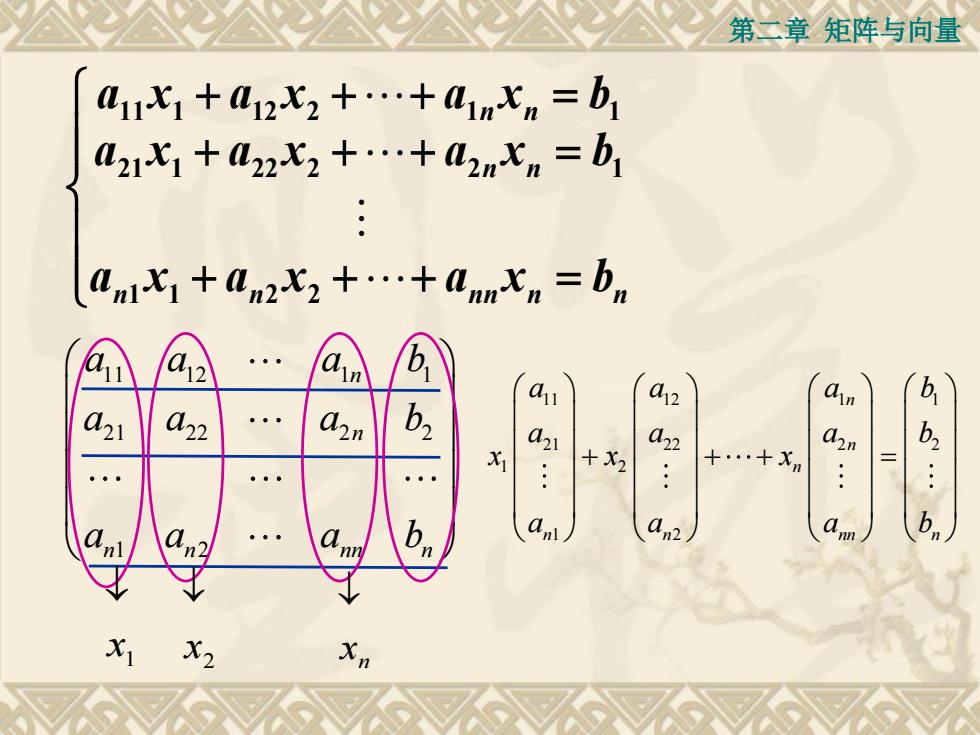
第二章矩阵与向量ax, +ai2x +...+ainxn = ba21i +a2X, +...+a2nX, =b=baniXi +an2X, +...+annXnnnbdind12allbanla2ainb2a22an1a2nb,a21a22azn+X2Xi+xn..6anlab.naa.nman2nlnnnXX

第二章 矩阵与向量                    n n n n n n n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 21 1 22 2 2 1 11 1 12 2 1 1 11 12 1 1 21 22 2 2 1 2 n n n n nn n a a a b a a a b a a a b             1 x  2 x  n x  11 12 1 1 21 22 2 2 1 2 1 2 n n n n n nn n a a a b a a a b x x x a a a b                                                    

第二章矩阵与向量一、n维向量概念定义2.2.1由n个数组成的有序数组(ai，a2，…an)称为一个n维向量α= (aj, az, ... an)其中第i个数a;（i=l,2,，n）称为n维向量α的第i个分量或坐标分量全为实数的向量称为实向量分量全为复数的向量称为复向量

第二章 矩阵与向量 由n个数组成的有序数组(a1 , a2 , . an )称为 一个n维向量.  = ( a1 , a2 , . an ) 其中第 i 个数 ai ( i = 1, 2, . , n ) 称为 n 维 向量  的第 i 个分量或坐标. 一、n维向量概念 定义2.2.1 分量全为复数的向量称为复向量. 分量全为实数的向量称为实向量

第二章矩阵与向量零向量0 =(0, 0, ... , 0)负向量一α=(一aj,一az,..,一an)(—ai,—a ..., —an)称为α=(ai, a,... an)的负向量.记为一αα= (a, a, ..., an)行向量

第二章 矩阵与向量 零向量 0 = ( 0, 0, . , 0 ) 负向量 ( －a1 , －a2 , ., －an )称为 = ( a1 , a2 , . an )的 负向量.记为－ . － = (－a1 , －a2 , ., －an ) 行向量  = ( a1 , a2 , ., an )