《线性代数》课程教学资源（课件讲稿，C）第四章 4-2齐次线性方程组

第四章线性方程组第二节齐次线性方程组

第四章 线性方程组 第二节 齐次线性方程组

第四章线性方程组一、齐次线性方程组解的性质设有齐次线性方程组ax +ax2 +..+ainn = 0a21 + a22X2 + ... + a2nxn = 0(1).+amx=0am1Xi+am2X2+anlXa12X2a21aAx = 0(2)1记 A=,x=a0m2mlmn

第四章 线性方程组 设有齐次线性方程组                    0 0 0 1 1 2 2 21 1 22 2 2 11 1 12 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     记 （1） 一、齐次线性方程组解的性质 11 12 1 1 21 22 2 2 1 2 , n n m m mn n a a a x a a a x A x a a a x                           Ax  0 (2)

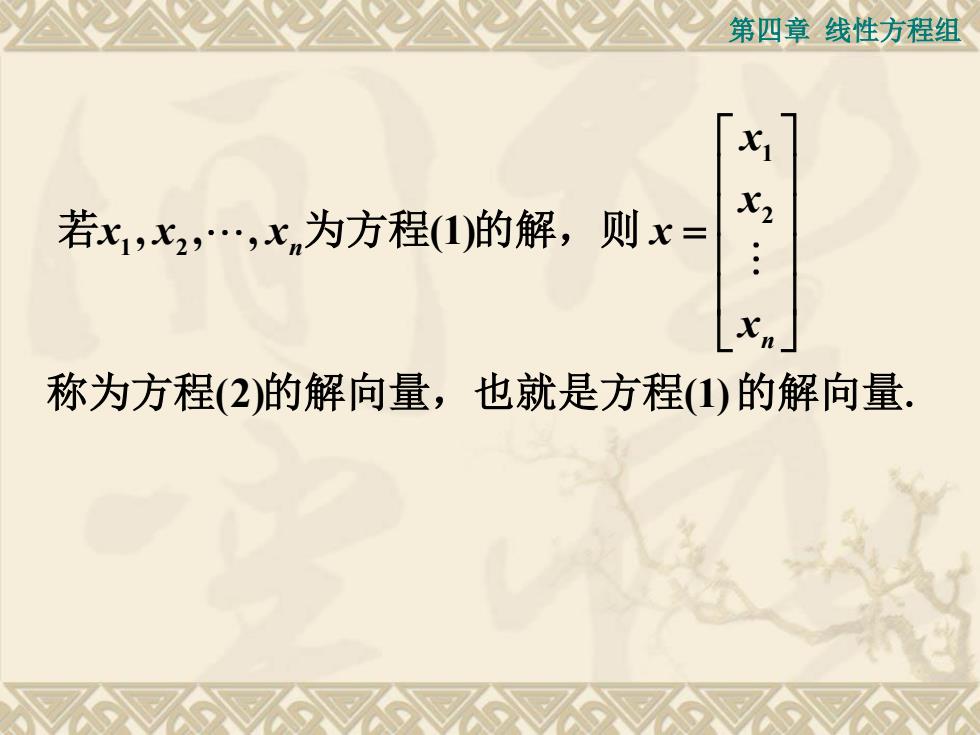
第四章线性方程组XX2若xi,X2,…,x,为方程(1)的解，则x=X称为方程(2)的解向量，也就是方程(1)的解向量

第四章 线性方程组 1 2 1 2 , , , (1) (2) (1) n n x x x x x x x              若 为方程 的解，则 称为方程 的解向量，也就是方程 的解向量

第四章线性方程组性质1两个解向量的和仍然是解向量，即设，5，是齐次线性方程组的解向量则5+5,也是齐次线性方程组的解向量证明：只需证明+，满足齐次线性方程组即可: A5i = 0, A52 = 0: A(E +5)= AS + A52 = 0故x=+5,也是Ax=0的解

第四章 线性方程组 1 2 1 2 , 1      两个解向量的和仍然是解向量， 即设 是齐次线性方程组的解向量， 则 也是齐次线性方程 性质 组的解向量. 证明：  A 1   2   A 1  A 2  0  A 1  0, A 2  0 故 x 也是Ax 0的解.   1   2    只需证明 1 2 + 满足齐次线性方程组即可

第四章线性方程组性质2一个解向量的倍数仍是解向量即设是齐次线性方程组的解向量，孔是任意数则入也是齐次线性方程组的解向量证明 ：A(5)=A(5)=20=0.：入也是齐次线性方程组的解向量说明：设引,52……，n-,是齐次线性方程组的解向量，a,22..an-是任意数，则a5i +252 +...+an-r5,Sn-仍是齐次线性方程组的解向量

第四章 线性方程组 2     一个解向量的倍数仍是解向量， 即设 是齐次线性方程组的解向量， 是任意数， 则 也是齐次线性方程组的 性质 解向量. 证明 A A     1 1       0 0.  也是齐次线性方程组的解向量 说明： 1 2 1 2 1 1 2 2 , , , , , n r n r n r n r                     设 是齐次线性方程组的解向量， 是任意数， 则 仍是齐次线性方程组的解向量