
知识回顾:向量的加减运算:a =(xi, Ji,z), b =(x2, y2,z2)→a±b =(xi ±x2,±2,Z ±z2)向量的数乘运算:a =(Xi, y1,z))Aa =(axi,nyi, nz))
向量的加减运算: 1 2 1 2 1 2 a b x x y y z z ( , , ) → → = 1 1 1 2 2 2 a x y z b x y z ( , , ), ( , , ) → → = = 向量的数乘运算: 1 1 1 a x y z ( , , ) → = 1 1 1 a x y z ( , , ) → = 知识回顾:
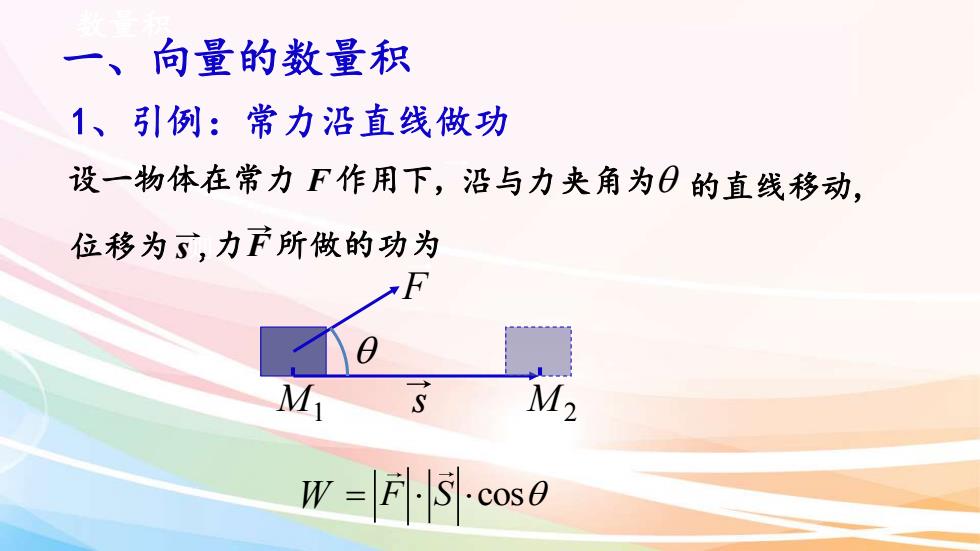
向量的数量积一1、引例:常力沿直线做功设一物体在常力F作用下,沿与力夹角为θ的直线移动,位移为,力F所做的功为F0MM2SW =|FlISlS.cos6
M1 1、引例:常力沿直线做功 沿与力夹角为 的直线移动, 设一物体在常力 F 作用下, F 位移为 s则,力F 所做的功为 M2 s W = F S cos 数量积 一、向量的数量积

2、数量积的定义及性质(1) 定义1 设向量,b的夹角为θ,称记作→→[a]|b|cos 0a. b→→为向量a,b 的数量积(也称为点乘积)
(1)定义1 设向量 a, b 的夹角为 ,称 2、数量积的定义及性质 a b cos 记作 a b → → 为向量 a b, → → 的数量积(也称为点乘积)

当a0时 b 在a上的投影为定义2记作16|cos 0Prjab60a故a.b=aPrj,b当6+0时a.b-|b|Prj, a
定义2 当 0 a b 记作 故 0 b a b b Prj b cos Prja b a b = a ba Prj a b = b a 时 , 在 a 上的投影为 当 时
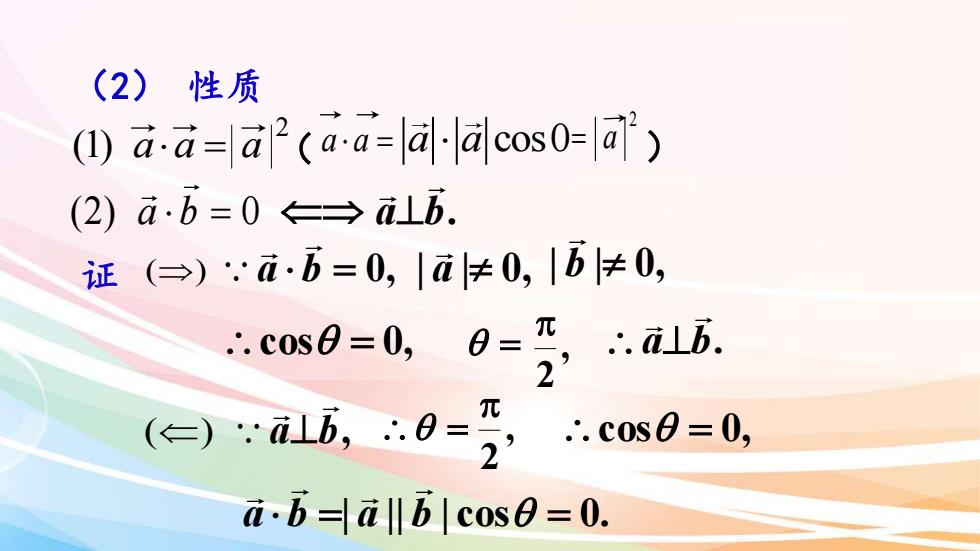
(2)性质(1) a.a=a2(a.a=al-lacoso=a)(2) a.b =0 <←=>alb.证 () :a.b=0, la0, lb0,元..alb.0:.. cosO = 0,2元() :alb, :.0::. cosO = 0,2a.b=|allblcoso=0
( 2 ) 性质 ( 1 ) a a = 2 a ( a a = a a cos0 2 = a ) ( 2 ) a b = 0 a b. ⊥ () a b = 0, | a | 0, | b | 0, cos = 0, a b. ⊥ () a b, ⊥ cos = 0, a b =| a || b | cos = 0. 证 = , 2 , 2 =