《线性代数》课程教学资源（课件讲稿，C）第四章 4-2齐次线性方程组

第四章线性方程组基础解系及其求法二、齐次方程组的全部解向量构成个一个向量空间称为齐次方程组的解空间.它是R"的一个子空间下面我们来求解空间的一个极大线性无关组设齐次线性方程组系数矩阵A的秩为r.不妨假设A的前r个列向量线性无关，于是A的行最简形为

第四章 线性方程组 二、基础解系及其求法 齐次方程组的全部解向量构成个一个向量空间, 称为齐次方程组的解空间. 它是R n的一个子空间. 下面我们来求解空间的一个极大线性无关组。 设齐次线性方程组系数矩阵A的秩为r,不妨假 设A的前r个列向量线性无关，于是A的行最简形为

第四章线性方程组b一1r+11.11bbrr+rn001与I对应的线性方程组为xLn(3)hhXr.r+l1r.n

第四章 线性方程组 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 r n rr rn b b b b I                              1 1, 1 1 1, , 1 1 , (3) r r n n r r r r r n n x b x b x x b x b x                  与I对应的线性方程组为

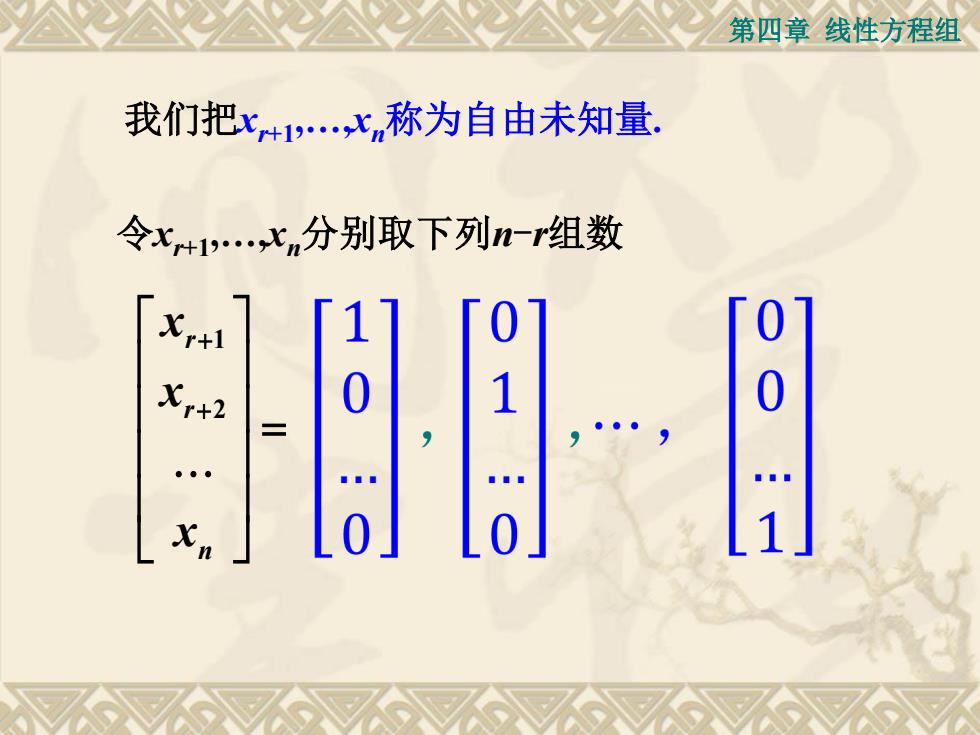
第四章线性方程组我们把x+1.…x,称为自由未知量.令xr+1.分别取下列n-r组数001+1001Xr+21O

第四章 线性方程组 我们把xr+1,.,xn称为自由未知量. 令xr+1,.,xn分别取下列n-r组数 1 2 r r n x x x                

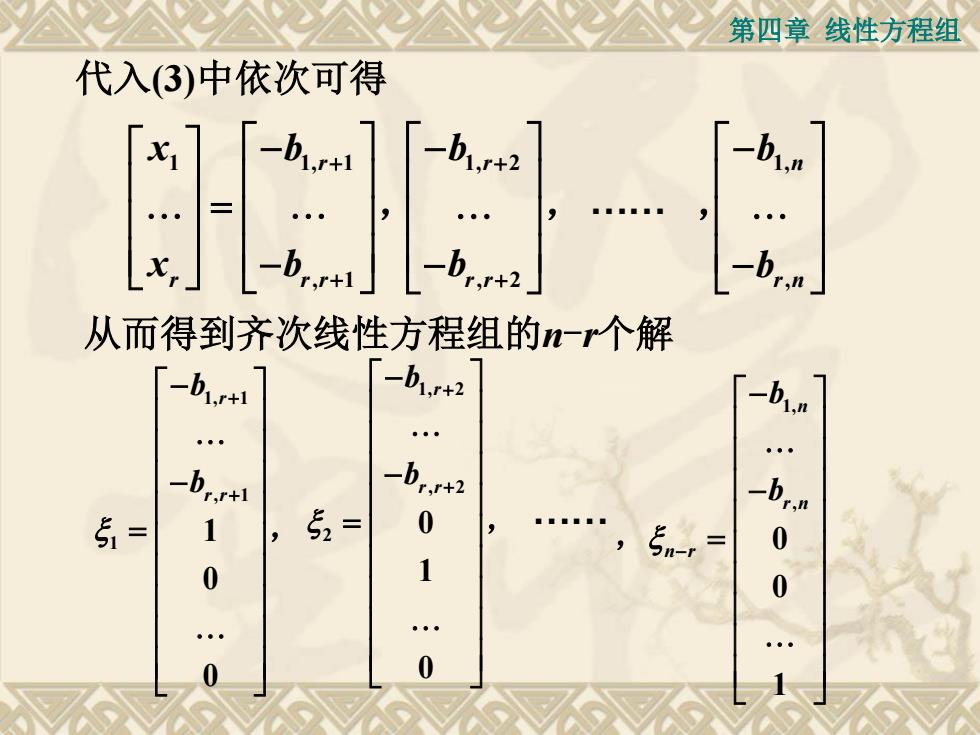
第四章线性方程组代入（3）中依次可得xh+r+.r+2+从而得到齐次线性方程组的n-r个解-b1,r+2-brt-h-b,r+2-b.r+r,n5=00

第四章 线性方程组 1 1, 1 , 1 r r r r x b x b                           ， 1, 2 , 2 r r r b b               ， 1, , n r n b b             ， 代入(3)中依次可得 . 从而得到齐次线性方程组的n-r个解 1, 1 , 1 1 1 0 0 r r r b b                               ， 1, 2 , 2 2 0 1 0 r r r b b                               ， 1, , 0 0 1 n r n n r b b                              ，