《线性代数》课程教学资源（课件讲稿，C）第二章 2-4矩阵的秩

第二章矩阵与向量第四节矩阵的秩

第二章 矩阵与向量 第四节 矩阵的秩

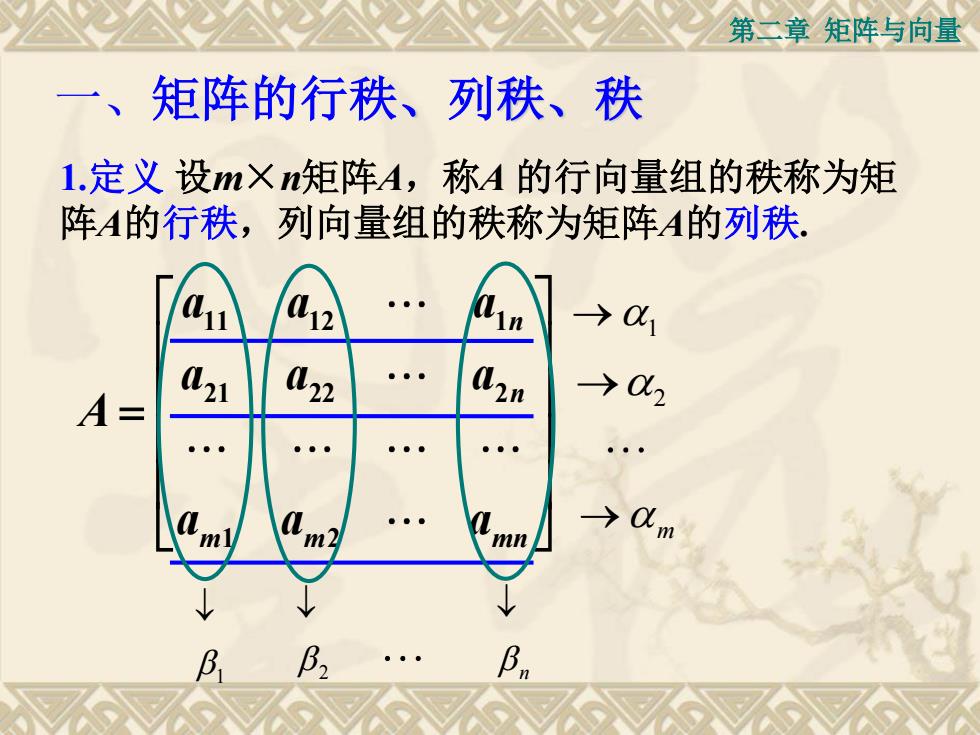
第二章矩阵与向量一、矩阵的行秩、列秩、秩1.定义设mXn矩阵A，称A的行向量组的秩称为矩阵A的行秩，列向量组的秩称为矩阵A的列秩W→αInaa221→α22n21A=→α00mmlm2mnβ,βB1

第二章 矩阵与向量 1.定义 设m×n矩阵A，称A 的行向量组的秩称为矩 阵A的行秩，列向量组的秩称为矩阵A的列秩. 一、矩阵的行秩、列秩、秩 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a              1 2  m 1   2   n 

第二章矩阵与向量0例1设矩阵A=12，求它的行秩和列秩2解： A的行向量α, =(1,0,1),α, =(0,1,2),α, =(2,1,4)0由行列式012=0，知向量组α,α,α,线性相关，21又α,α,线性无关，故α,α,是A的行向量组的一个最大无关组，所以矩阵A的行秩等于2

第二章 矩阵与向量 1 0 1 1 0 1 2 2 1 4 A            例 设矩阵 ，求它的行秩和列秩 1 2 3 A的行向量      (1,0,1), (0,1,2), (2,1,4) 1 2 3 1 0 1 0 1 2 0 , , 2 1 4 由行列式  ，知向量组   线性相关， 解： 1 2 1 2 , , 2. A A 又    线性无关，故 是 的行向量组的一个 最大无关组，所以矩阵 的行秩等于

第二章矩阵与向量3111例2 求矩阵A=2的行秩和列秩01000解：A的行向量α, =(1,1,3,1),α, =(0,2,-1,4),α, = (0,0, 0,5)去掉第三个分量的α, =(1,1,1),α, =(0,2,4),α, =(0,0,5)L由行列式0=10±0，知向量组α,α,α线性无关21500所以A的行秩为3向量组α,αz,α,也线性无关

第二章 矩阵与向量 1 2 3 A的行向量       (1,1,3,1), (0,2, 1,4), (0,0,0,5) 1 1 3 1 2 0 2 1 4 0 0 0 5 A             例 求矩阵 的行秩和列秩 解： 1 2 3 去掉第三个分量的         (1,1,1), (0,2,4), (0,0,5) 1 2 3 111 0 2 4 10 0 , , 005 由行列式   ，知向量组     线性无关. 1 2 3 向量组   , , 也线性无关 所以A的行秩为3

第二章矩阵与向量31A的列向量组β,=|0β, =2β, =-1β =4LO]0504个三维向量必线性相关，而其中ββ线性无关所以A的列秩也等于3

第二章 矩阵与向量 1 2 3 4 1 1 3 1 0 2 1 4 0 0 0 5 A                                                  的列向量组 4个三维向量必线性相关，而其中β1 β2 β4线性无关， 所以A的列秩也等于3