
3.1解的存在唯一性定理与逐步逼近法 任取一个连续函数,(x)代入积分方程右端的>,得函数 9(x)=y+Jf(s,0,(s)函 注 这里取的P,(x的图象必须在区域R内.因此x-x≤h 时,必须有p,(x)-y≤b成立,否则fx,m,(x)有可能无定义 如果0(x)=(x),那么()就是积分方程的解。否则,再把 ,(x)代入积分方程中右端的y,得到 (可以证明p(x) ,(x)=+∫f(s,9s)b 在区域R内) 如果P2(x)三(x),那么9(x)就是积分方程的解,否则我们继 续这个步骤,一般地作函数 p(x)=y+f(s,pn1(s)达 (2.4) 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 任取一个连续函数 0 ( ) x 代入积分方程右端的 y , 得函数 = + ( ) 0 1 0 0 ( ) , ( ) x x x y f s s ds ( ) 0 2 0 1 ( ) , ( ) x x x y f s s ds = + 如果 那么 就是积分方程的解。否则,再把 代入积分方程中右端的 ,得到 1 0 ( ) ( ), x x 1 ( ) x y 0 ( ) x (可以证明 在区域R内) ( ) 1 x 如果 ,那么 就是积分方程的解,否则我们继 续这个步骤,一般地作函数 2 1 ( ) ( ) x x 1 ( ) x = + ( − ) 0 0 1 ( ) , ( ) (2.4) x n n x x y f s s ds 这里取的 的图象必须在区域R内. 因此 时, 必须有 否则 有可能无定义 − 0 x x h 0 0 ( ) x y b − 成立, 0 f x x ( , ( )) 0 注 ( ) x §3.1 解的存在唯一性定理与逐步逼近法

3.1解的存在唯一性定理与逐步逼近法 就得到连续函数序列: p1(x)3p2(x),.pn(x)y。 如果p+1(x)=pn(x)那么pn(x)就是积分方程的解。 如果始终不发生这种情况,可以证明函数,p2,P.一致 收敛于p(x),然后证明这个极限函数p(x)就是积分方程(2.4) 的解.此方法称为逐步逼近法;(2.4)称为第n次近似解。 以下只在右半区间[,七,+月上讨论,左半区间上的讨论类似 命题1.设y=p(x)是(2.1)定义于[x,x+止满足 0(x)=y0 (2.3) 的解,则y=p(x)是积分方程 y=+f(s,p(s)达 (2.5) 的定义在x,x+M上的连续解。反之,如果=p(x)是积分方程(2.5) 定义在[x。,x。+h]上的连续解,则y=(x是微分方程(2.1)定义在上 [x,x+列满足2.3)的解. 结束 帮助 首而
结束 帮助 上一页 返回 下一页 目录 首页 如果始终不发生这种情况,可以证明函数列 一致 收敛于 ,然后证明这个极限函数 就是积分方程(2.4) 的解.此方法称为逐步逼近法;(2.4)称为第n次近似解。 1 2 , ,., ,. n ( ) x ( ) x 就得到连续函数序列: 1 2 ( ), ( ),. ( ),. n x x x n n +1 ( ) ( ) x x = ( ) n 如果 ,那么 x 就是积分方程的解。 以下只在右半区间 x x h 0 0 , + 上讨论,左半区间上的讨论类似. §3.1 解的存在唯一性定理与逐步逼近法 y x =( ) y x =( ) + 0 0 [ , ] x x h = 0 0 ( ) (2.3) x y = + ( ) 0 0 , ( ) (2.5) x x y y f s s ds + 0 0 命题1. 设 是(2.1)定义于 [ , ] x x h 上满足 的解,则 是积分方程 的定义在 上的连续解。反之,如果 是积分方程(2.5) 定义在 上的连续解, 则 是微分方程(2.1)定义在上 满足(2.3)的解. y x = ( ) 0 0 [ , ] x x h + y x = ( ) 0 0 [ , ] x x h +
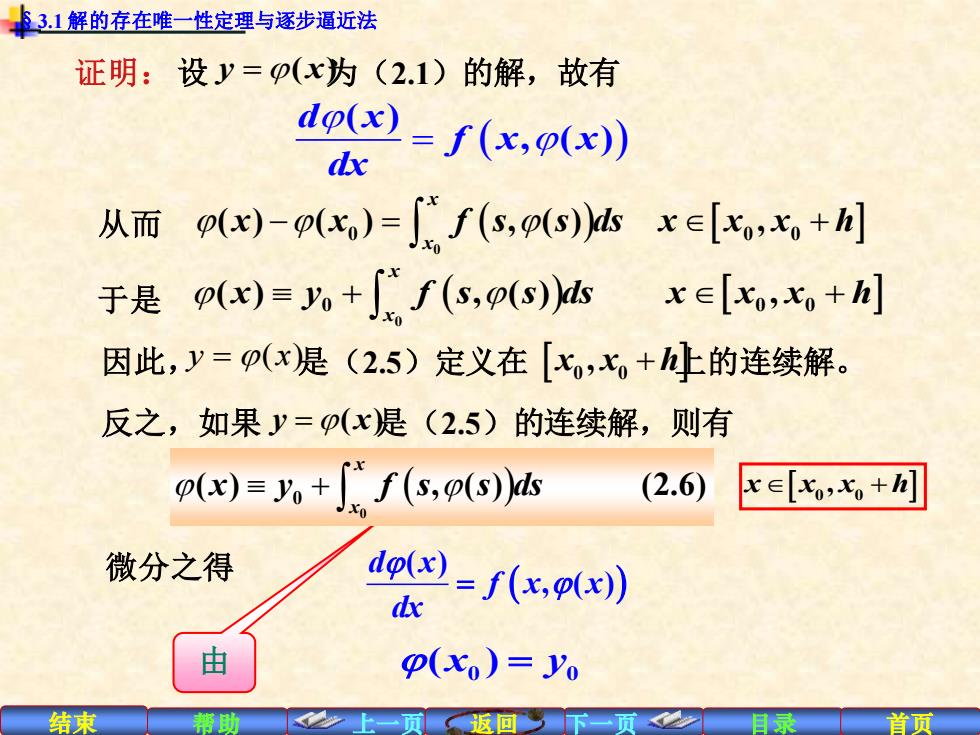
®31解的存在唯一性定理与逐步逼近法 证明:设y=p(x为(2.1)的解,故有 do)=f(x,p(x) dx 从而p()-(x,)=f(s,(s)hx∈[,七+ 于是(x)=+f(s,p(s) x∈[xo,x+h] 因此,y=(x是(2.5)定义在[七,七+的连续解。 反之,如果y=p(x是(2.5)的连续解,则有 (x)=yo+["f(s,o(s)ds (2.6 x∈[xo,x+h] 微分之得 do( d 2=f(x,p(x) 由 P(xo)=Yo 结束 帮助 返回
结束 帮助 上一页 返回 下一页 目录 首页 由 证明:设 y x =( ) 为(2.1)的解,故有 ( ) = ( ) , ( ) d x f x x dx 因此, y = (x) 是(2.5)定义在 x x h 0 0 , + 上的连续解。 反之,如果 y x =( ) 是(2.5)的连续解,则有 微分之得 ( ) ( ) , ( ) d x f x x dx = 0 0 ( ) x y = 于是 + + ( ) 0 0 0 0 ( ) , ( ) , x x x y f s s ds x x x h − = + ( ) 0 0 0 0 ( ) ( ) , ( ) , x x 从而 x x f s s ds x x x h + ( ) 0 0 ( ) , ( ) (2.6) x x x y f s s ds x x x h + 0 0 , §3.1 解的存在唯一性定理与逐步逼近法
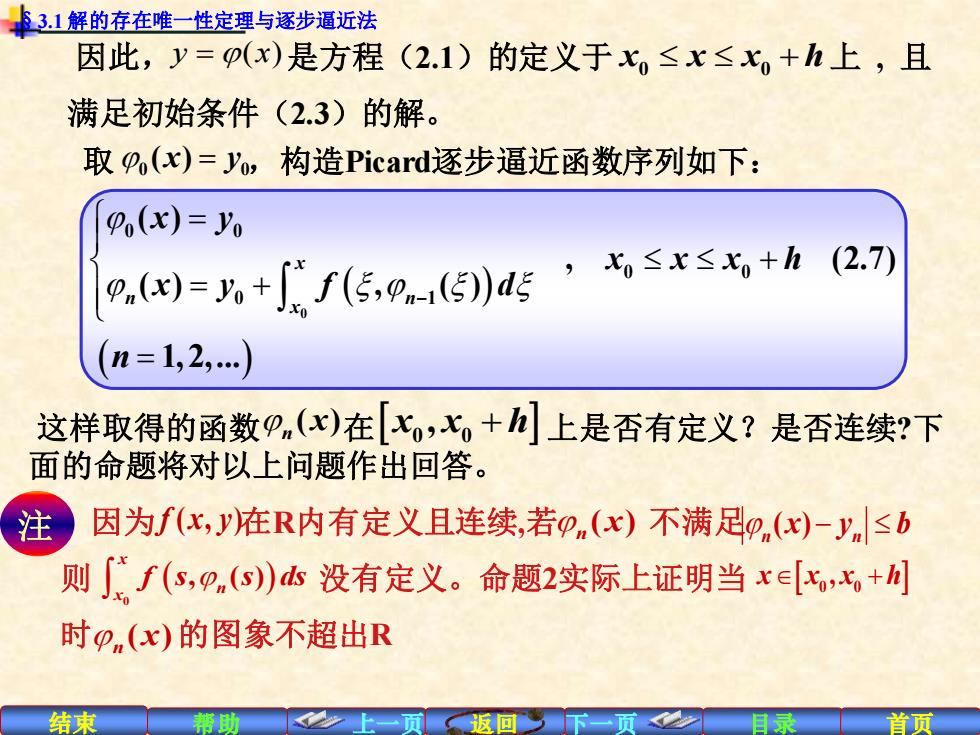
3.1解的存在唯一性定理与逐步逼近法 因此,y=p(x)是方程(2.1)的定义于x,≤x≤x,+h上,且 满足初始条件(2.3)的解。 取p(x)=yo,构造Picard逐步逼近函数序列如下: Po(x)=Yo .(=八+f((5,0n1传)d5’七≤x≤x+h(2.7 n=1,2,.) 这样取得的函数p(x)在[xo,x,+h上是否有定义?是否连续?下 面的命题将对以上问题作出回答。 注 因为fc,y在R内有定义且连续,若p(x)不满足D(x)-yn≤b 则∫f(s,p(s)心没有定义。命题2实际上证明当x∈[s,x+川 时p(x)的图象不超出R 结束 首页
结束 帮助 上一页 返回 下一页 目录 首页 因此, 是方程(2.1)的定义于 上 , 且 满足初始条件(2.3)的解。 y = (x) x x x h 0 0 + 取 0 0 ( ) x y = ,构造Picard逐步逼近函数序列如下: ( ) ( ) − = + = + = 0 0 0 0 0 0 1 ( ) , (2.7) ( ) , ( ) 1, 2,. x n n x x y x x x h x y f d n 这样取得的函数 在 上是否有定义?是否连续?下 面的命题将对以上问题作出回答。 因为 在R内有定义且连续,若 不满足 则 没有定义。命题2实际上证明当 时 的图象不超出R ( ) n x x x h 0 0 , + ( ) n x ( )− n n x y b ( ) 0 , ( ) x n x f s s ds x x x h + 0 0 , ( ) n x 注 f x y ( , ) §3.1 解的存在唯一性定理与逐步逼近法

3.1解的存在唯一性定理与逐步逼近法 命题2.对于所有的正整数n,(2.7)中的p(x)在[Xo,x,+h上有定义, 连续且满足 pn(x)-y≤b (2.8) 证明:用数学归纳法证明。当=1时 m,(x)=+Jf(5y)15 ,(x)在[x,x+小上有定义,连续且 lA,(x)-l≤f5,)lh5≤M(x-x)≤Mh≤b 即命题2当n=1时成立.设当=k时,p(x)在[xo,x+h上有定 义,连续且满足 9(x)-ya≤b 这时 P+1(x)=o+f(5,P(5)15 结束 帮助 返叵
结束 帮助 上一页 返回 下一页 目录 首页 命题2. 对于所有的正整数n, (2.7)中的 在 上有定义, 连续且满足 ( ) n x x x h 0 0 , + − 0 n ( ) 2.8 x y b ( ) 证明:用数学归纳法证明。当n=1 时 ( ) 0 1 0 0 ( ) , x x x y f y d = + 1 ( ) x 在 x x h 0 0 , + 上有定义,连续且 1 0 ( ) x y − 即命题2 当 n=1 时成立. 设当n=k时, 在 上有定 义,连续且满足 ( ) k x x x h 0 0 , + − 0 ( ) k x y b ( ) 0 1 0 ( ) , ( ) x k k x + x y f d = + 这时 §3.1 解的存在唯一性定理与逐步逼近法 0 0 ( , ) x x f y d − M x x Mh ( 0 ) b