
导航 2填空: (1)零点的定义:一般地,如果函数y=fx)在实数a处的函数值等 于,即 ,则称a为函数y=fx)的零点 (2)a是函数fx)零点的充分必要条件是,(α,0)是函数图象与 的公共点
导航 2.填空: (1)零点的定义:一般地,如果函数y=f(x)在实数α处的函数值等 于零,即 f(α)=0 ,则称α为函数y=f(x)的零点. (2)α是函数f(x)零点的充分必要条件是,(α,0)是函数图象与 x轴 的公共点
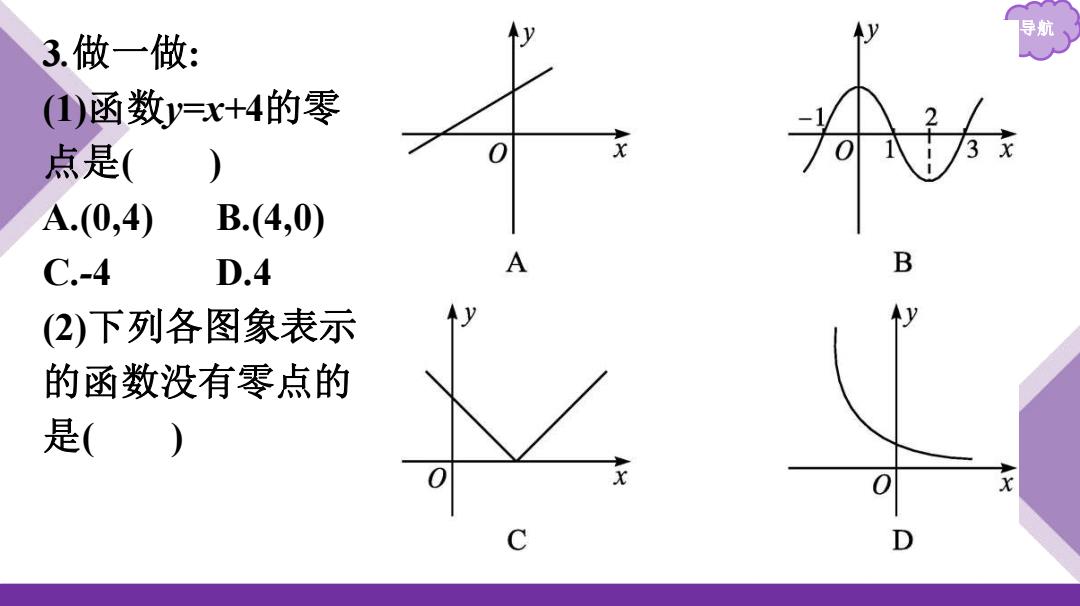
3.做一做: (1)函数y=x+4的零 点是( A.(0,4) B.(4,0) C.-4 D.4 A (2)下列各图象表示 的函数没有零点的 是() X C D
导航 3 .做一做 : (1)函数y=x+ 4的零 点是 ( ) A.(0,4) B.(4,0) C.-4 D.4 (2)下列各图象表示 的函数没有零点的 是( )

导航、 解析:1)令x+4=0,得x=-4,所以函数的零点为-4, (2)因为选项D中的函数图象与x轴没有公共点, 所以其表示的函数没有零,点 答案:1)C(2)D
导航 解析:(1)令x+4=0,得x=-4,所以函数的零点为-4. (2)因为选项D中的函数图象与x轴没有公共点, 所以其表示的函数没有零点. 答案:(1)C (2)D

导 二、二次函数的零点及其与对应方程、不等式解集之间的关 系 【问题思考】 1.考查下列一元二次方程与对应的二次函数: ①方程x2-2x-3=0与函数y=x2-2x-3; ②方程x2-2x+1=0与函数y=x2-2x+1; ③方程x2-2x+3=0与函数y=x2-2x+3
导航 二、二次函数的零点及其与对应方程、不等式解集之间的关 系 【问题思考】 1.考查下列一元二次方程与对应的二次函数: ①方程x 2 -2x-3=0与函数y=x2 -2x-3; ②方程x 2 -2x+1=0与函数y=x2 -2x+1; ③方程x 2 -2x+3=0与函数y=x2 -2x+3

()请列表表示出方程的根、函数的图象及图象与x轴交点的航 坐标 提示: 方程 x2-2x-3=0 x2.2x+1=0 c2-2x+3=0 函数 y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 y y 2 函数的 1 o 图象 -123x 2 -2 -10123x 1 -10123x
导航 (1)请列表表示出方程的根、函数的图象及图象与x轴交点的 坐标. 提示: 方程 x 2 -2x-3=0 x 2 -2x+1=0 x 2 -2x+3=0 函数 y=x2 -2x-3 y=x2 -2x+1 y=x2 -2x+3 函数的 图象