
全程设计 2.2.3 一元二次不等式的解法
2.2.3 一元二次不等式的解法
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解一元二次不等式的概念 2.掌握解一元二次不等式的两种方法:因式分解法和配方法. 3.会解简单的分式不等式 4.加强逻辑推理和数学运算能力的培养
导航 课标定位素养阐释 1.了解一元二次不等式的概念. 2.掌握解一元二次不等式的两种方法:因式分解法和配方法. 3.会解简单的分式不等式. 4.加强逻辑推理和数学运算能力的培养

导航 课前·基础认知 一元二次不等式的概念 【问题思考】 1.下列式子是关于x的不等式,且x的最高次幂为2的 是 (填序号) ①x2+2x-1=0;②x2≤5; ③x2.3<2x; ④x-1>4-2x. 提示:②
导航 课前·基础认知 一、一元二次不等式的概念 【问题思考】 1.下列式子是关于x的不等式,且x的最高次幂为2的 是 .(填序号) ①x 2+2x-1=0; ②x 2≤5; ③ax2 -3<2x; ④x-1>4-2x. 提示:②
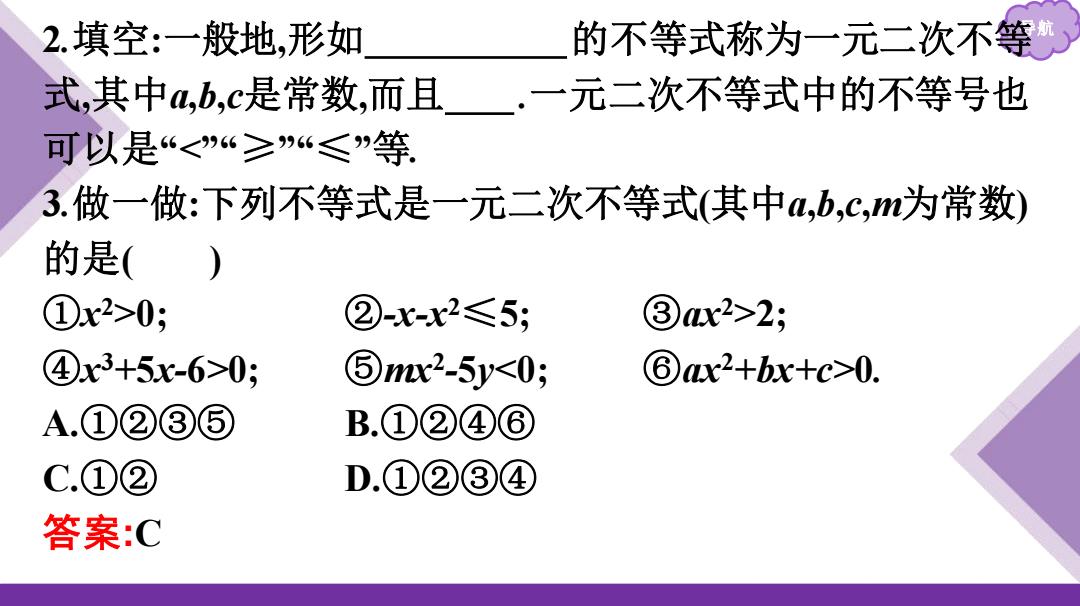
2.填空:一般地,形如 的不等式称为一元二次不等 式,其中,b,c是常数,而且·一元二次不等式中的不等号也 可以是“<“≥”“≤”等 3.做一做:下列不等式是一元二次不等式(其中a,b,c,m为常数) 的是( ①x2>0; ②-x-x2≤5; ③x2>2; ④x3+5x-6>0; ⑤mx2-5y<0; ⑥x2+bx+c>0. A.①②③⑤ B.①②④⑥ C.①② D.①②③④ 答案:C
导航 2.填空:一般地,形如ax2+bx+c>0 的不等式称为一元二次不等 式,其中a,b,c是常数,而且 a≠0 .一元二次不等式中的不等号也 可以是“<”“≥”“≤”等. 3.做一做:下列不等式是一元二次不等式(其中a,b,c,m为常数) 的是( ) ①x 2>0; ②-x-x 2≤5; ③ax2>2; ④x 3+5x-6>0; ⑤mx2 -5y<0; ⑥ax2+bx+c>0. A.①②③⑤ B.①②④⑥ C.①② D.①②③④ 答案:C