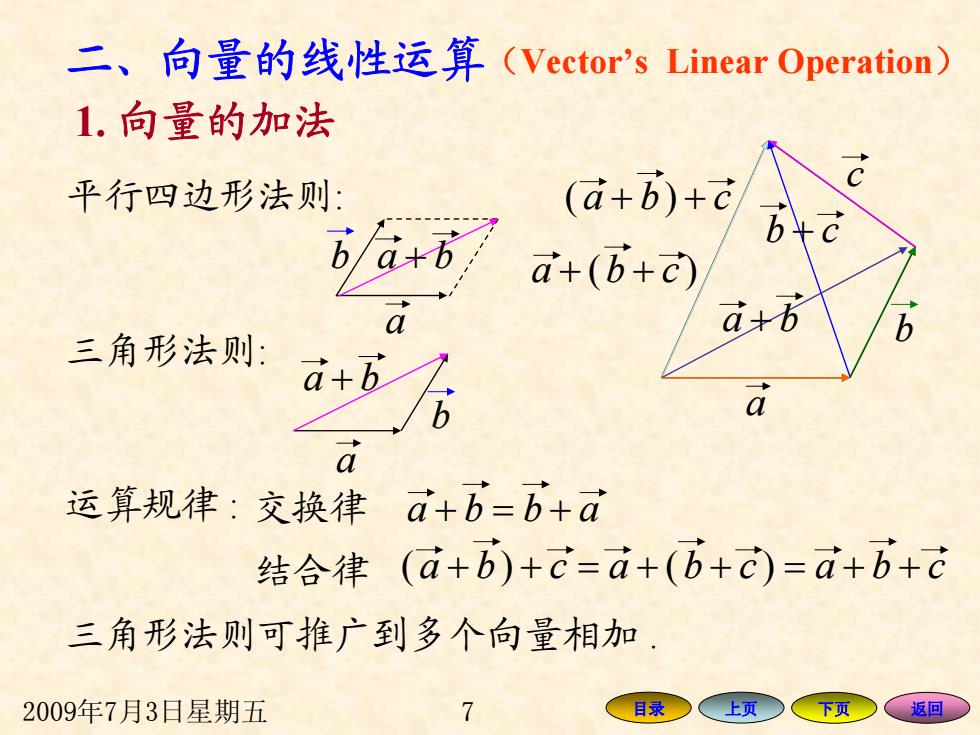
二、向量的线性运算(Vector's Linear Operation) 1.向量的加法 平行四边形法则: (a+B)+c a+6 a+(b+c) a 立+6 b 三角形法则: a a 运算规律:交换律 a+b-b+a 结合律(a+b)+c=a+(b+)=d+b+c 三角形法则可推广到多个向量相加 2009年7月3日星期五 7 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 二、向量的线性运算 1. 向量的加法 平行四边形法则: 三角形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . b b + = + abba + )( + cba = + + cba )( = + + cba a b c + ba + cb + + cba )( + )( + cba a a + ba + ba (Vector’s Linear Operation )
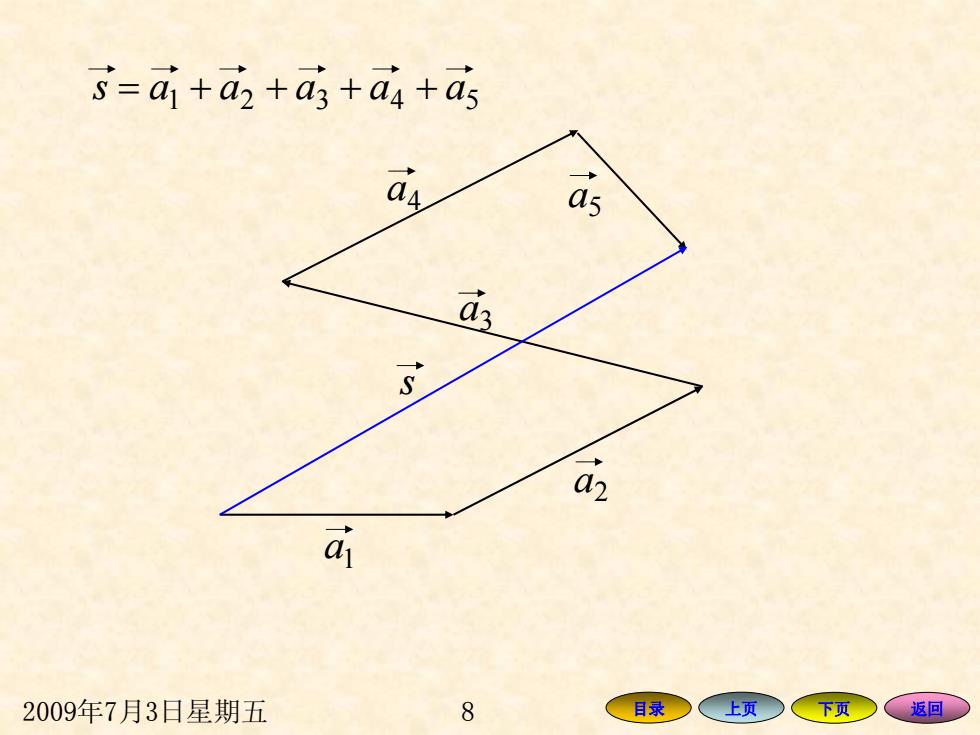
s-aj+a2 +a3+as+as as a2 2009年7月3日星期五 8 目录 (上页今 下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 s 3 a 4 a 5 a 2 a 1 a 54321 s = + + + + aaaaa
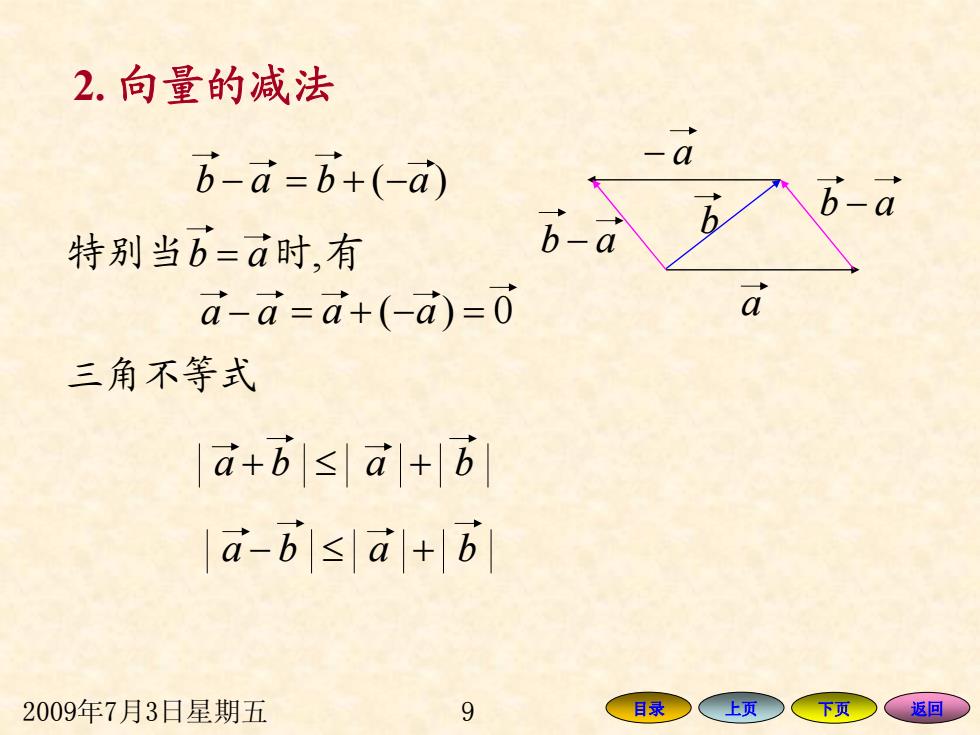
2.向量的减法 b-a-b+(-a) b b-a 特别当b=a时,有 a-a=a+(-a)-0 a 三角不等式 a+b≤d+b a-bs a+b 2009年7月3日星期五 9 目录○ 上页下页 、返回
2009年7月3日星期五 9 目录 上页 下页 返回 三角不等式 − ab = + −ab )( 特别当 = ab ,有时 − aa = + −aa )( + ≤ + baba − ab a b − ab − a = 0 − ≤ + baba 2. 向量的减法

3.向量与数的乘法 )是一个数,入与d的乘积是一个新向量,记作九d. 规定:>0时,入a与a同向,d=2d; 2<0时,a与d反向,2d=-a; 九=0时,a=0. 总之: xa =aa 运算律:结合律(ud)=u(2d)=ud 分配律(+)a=九d+ud 2(ā+b)=元ā+b 若a#0,则有单位向堂d-可a因此a=ad 2009年7月3日星期五 10 目录 上页 下页 、返回
2009年7月3日星期五 10 目录 上页 下页 返回 aaG G λ = λ λ 是一个数 , a . G λ 规定 : λ > 0 时, 与aa 同向, G G λ λ < 时,0 λ = 时,0 .0 G G λ a = aa ; G G λ = λ aa ;1 G G = 可见 aa ;1 G G − = − aa ; G G λ = − λ λ 与 a 的乘积是一个新向量, 记作 与aa 反向, G G λ 总之: 运算律 : 结合律 a)( G λ μ a)( G = μ λ a G = λ μ 分配律 a G λ+ μ)( aaG G = λ + μ ba )( G G λ + ba G G = λ + λ ,0 G G 若 a ≠ = G D 则有单位向量 a . 1 a a G G 因此 G G G D = aaa 3. 向量与数的乘法

定理1设a为非零向量,则 aW6三b=1a(?为唯一实数) 证:“一设a/6取入=±d,a,6同向时 取正号,反向时取负号,则b与入同向,且 d-小 故b=a. 再证数入的唯一性.设叉有=ua,则(2-)a=0 而a≠0,故2-4=0,即2=4. 2009年7月3日星期五 11 目录 上页 下页 返回
2009年7月3日星期五 11 目录 上页 下页 返回 设 a 为非零向量 , 则 ( λ 为唯一实数 ) 证 : “ ”. , 取 λ=± 且 再证数 λ 的唯一性 . 则 故 λ − μ = ,0 即 λ = μ . a ∥ b = λ ab 设 a ∥ b b a 取正号, 反向时取负号, , a , b 同向时 则 b 与 λ a 同向, 设又有 b = μ a , λ − μ a = 0)( λ a = λ a = b a a = b 故 = λ ab . 而 a ≠ ,0 定理1