《高等数学》课程教学资源（课件讲稿）第七章 微分方程_7-5 可降阶高阶微分方程

第五节 第七章 可降阶高阶微分方程 一、ym)口f(x)型的微分方程 二、y四f(x,yD型的微分方程 三、y□f(y,y)型的微分方程

可降阶高阶微分方程 第五节 一、 型的微分方程 二、 型的微分方程 三、 型的微分方程 第七章

一、ym口f(x)型的微分方程 令z口yaa,则口y四口f(x,因此 dx zD(x)dx口C 即 yma)口☐(x)dxC 同理可得 得ynm)D(x)dx C dx0C2 (x)dx [dx OCxC2 依次通过n次积分，可得含n个任意常数的通解

一、 令 因此 即 同理可得 依次通过 n 次积分, 可得含 n 个任意常数的通解 . 型的微分方程

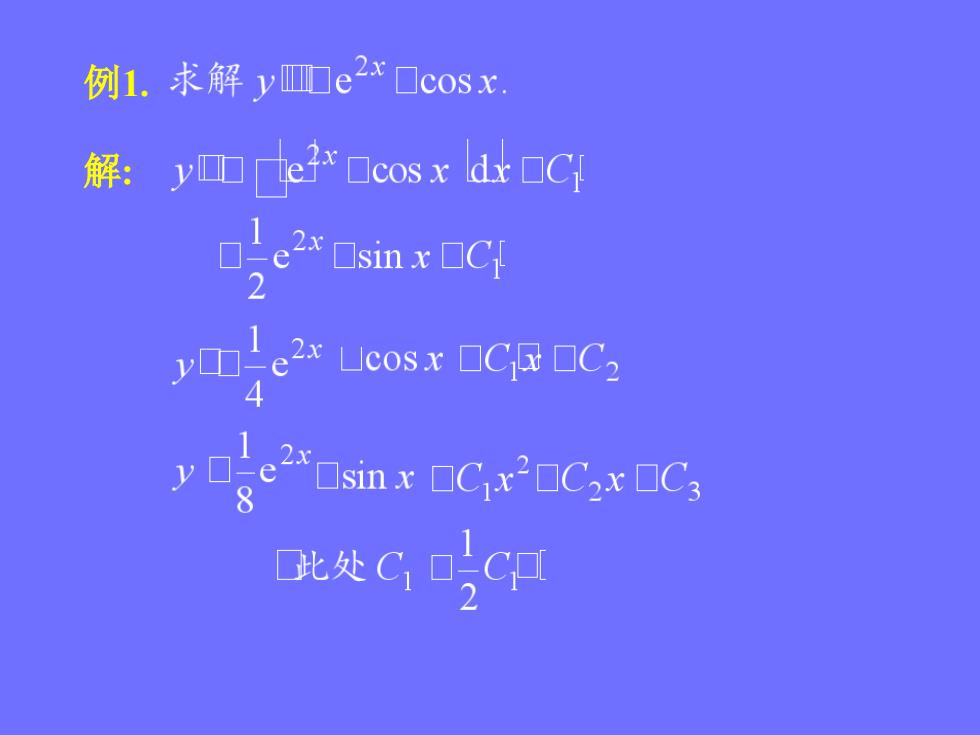
例1.求解y☐e2x口cosx 解：yDex☐cosx d☐C e2 sin x CC 2 ex Leosx CC2 4 2x yesin x Cx2C2xC3 此处cgc刚

例1. 解:

二、y中f(x,y5型的微分方程 设yDp(x),则y口p5原方程化为一阶方程 pf(x,p) 设其通解为 p□0(x,C1） 则得 y(x,C) 再一次积分，得原方程的通解 y(x,C)dx C2

型的微分方程 设 原方程化为一阶方程 设其通解为 则得 再一次积分, 得原方程的通解 二

例2.求解 (1□x)yD2xy yxo,y中xw3 解：设y巴p(x),则y四p5代入方程得 (1x2)p2xp 分离变量 dp 2xdx p (1☐x2) 积分得1np□ln(1口x)□lnC,即paC1(1☐x2) 利用y中0☐3，得C1□3，于是有y☐3(1口x2) 两端再积分得y口x3☐3x0C 利用yxo☐1，得C2☐l,因此所求特解为 y0x3☐3xO1

例2. 求解 解: 代入方程得 分离变量 积分得 利用 于是有 两端再积分得 利用 因此所求特解为