
4.数量积的坐标表示设a=axi+ayj+a,k,b=bi+bj+b,k,则a.b=(a,i+a, j+a, k).(b,i+b, j+b,k).i=j.j=k.=l,i.j=j.k=k.i=0a.b=axbx+a,b,+a,b两向量的夹角公式当a,b为非零向量时,由于a.=abcos,得a,bx +a,b, +a.b.a.bcOsO一ailbb,+bHIGH EDUCATION PRESS上页下页返回结束机动自录
4. 数量积的坐标表示 设 则 = 0 x x y y z z = a b + a b + a b 当 为非零向量时, cos = = x x y y z z a b + a b + a b 2 2 2 x y z a + a + a 2 2 2 x y z b + b + b 由于 a b cos a a i a j a k , = x + y + z b b i b j b k , = x + y + z ( a i + a j + a k ) x y z ( b i b j b k ) x + y + z i j = j k = k i a b a b 两向量的夹角公式 , 得 机动 目录 上页 下页 返回 结束

例2. 已知三点 M(1,1,1), A(2,2,1),B(2,1,2), 求ZAMB解:MA=(1, 1, 0), MB =(1, 0,1)BCOS LAMB=_MA.MBM则MAMB1+0+0V2 V22元故AMB=3HIGH EDUCATION PRESS机动上页下页返回结束自录
M A = ( ), M B = ( ) = B M 例2. 已知三点 M (1,1,1), A( 2 , 2 ,1) , B( 2 ,1 , 2 ), AMB . A 解: 1, 1, 0 1, 0, 1 则 cos AMB = 1+ 0 +0 2 2 AMB = 求 M A M B MA MB 故 机动 目录 上页 下页 返回 结束
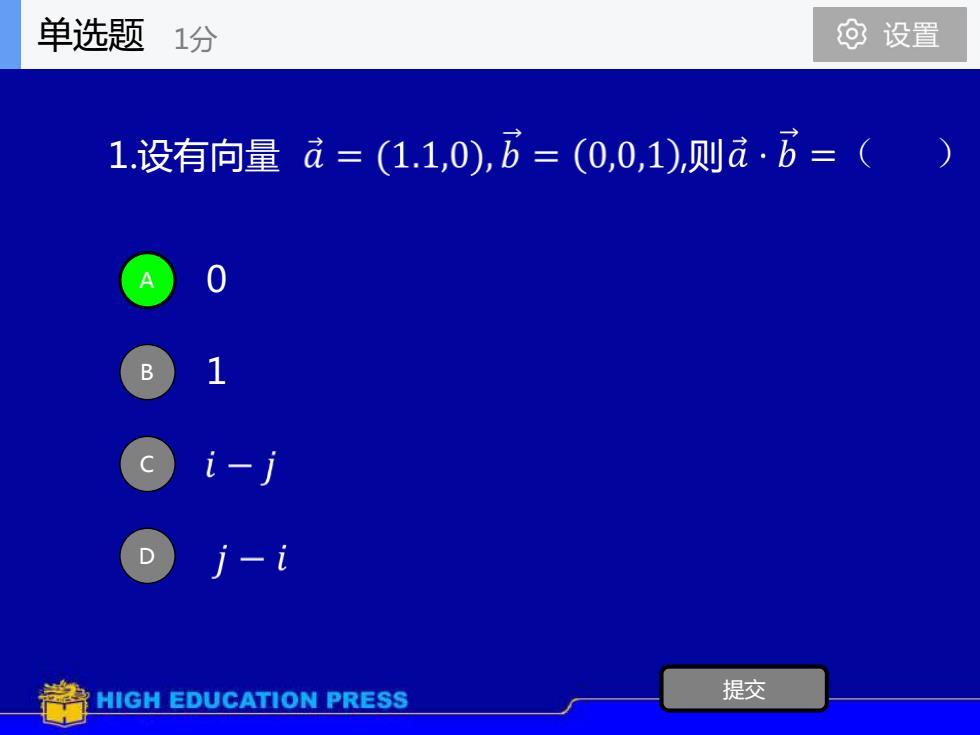
单选题0设置1分a= (1.1,0),b = (0,0,1),则a. b = ( 1.设有向量O1B一提交HIGH EDUCATION PRESS
1.设有向量 ,则 A 0 B 1 C D 提交 单选题 1分
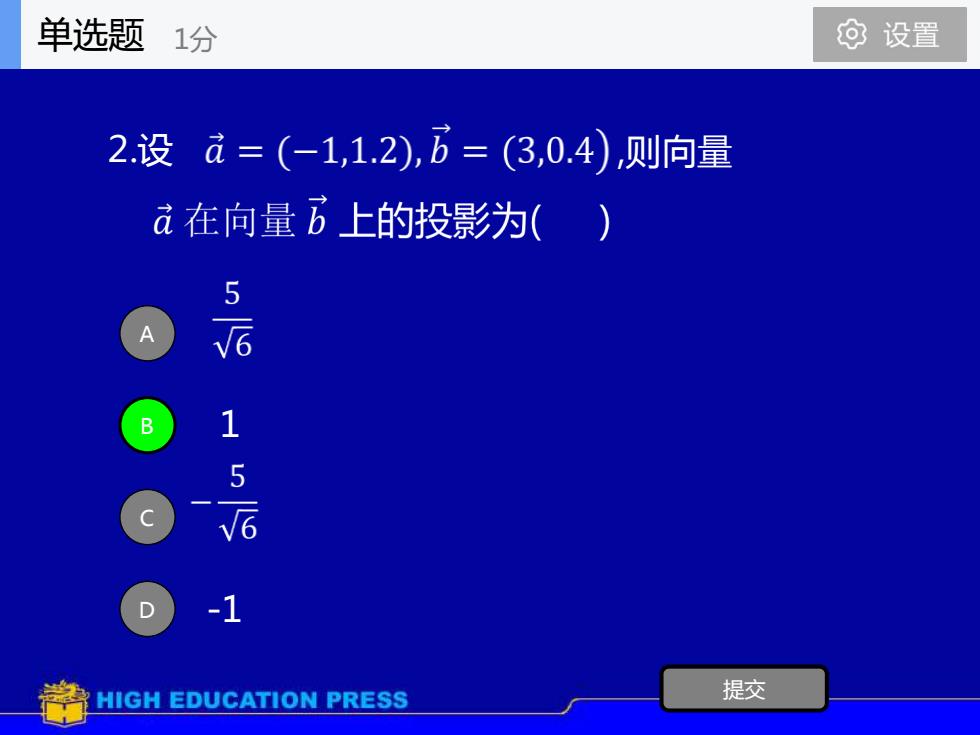
单选题0设置1分2.设a = (-1,1.2),b = (3,0.4),则向量a在向量 b 上的投影为(5T615V6提交HIGH EDUCATION PRESS
2.设 ,则向量 A B 1 C D -1 提交 单选题 1分
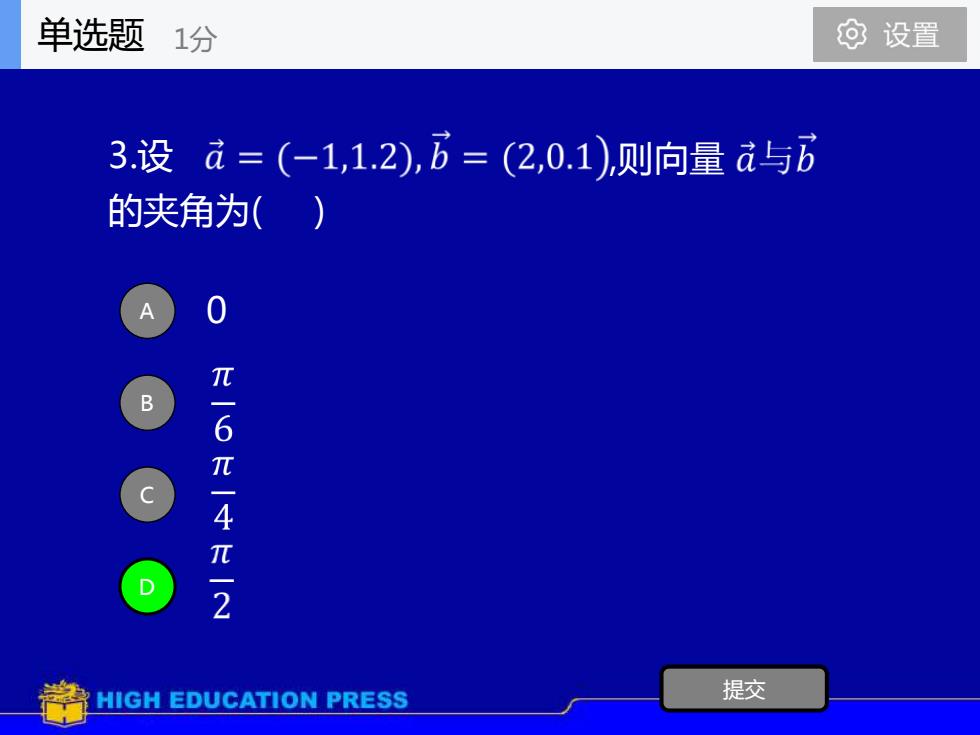
单选题0设置1分3.设a = (-1,1.2),b = (2,0.1),则向量 a与b的夹角为(元-6元-4元-2B提交HIGH EDUCATION PRESS
3.设 ,则向量 的夹角为( ) A 0 B C D 提交 单选题 1分