
全程设计 第四章 指数数与对数数 4.4对数函数 第2课时 对数函数的图象与性质
第四章 指数函数与对数函数 4.4 对数函数 第2课时 对数函数的图象与性质

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
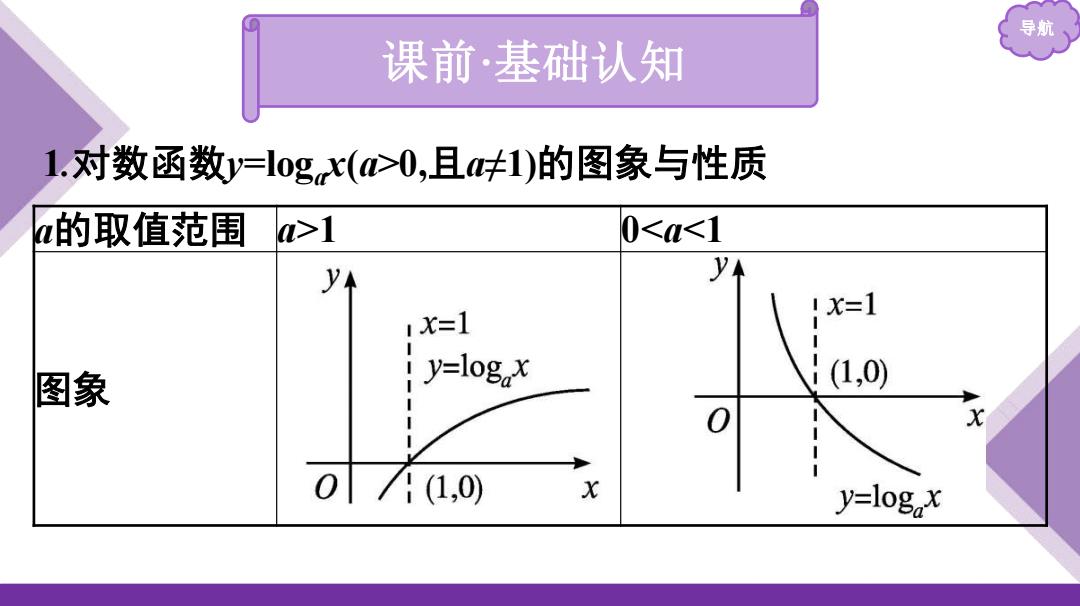
导航、 课前·基础认知 1.对数函数y=logx(a心>0,且呋1)的图象与性质 的取值范围 a>1 0<a<1 A y !x=1 1x=1 图象 y=logx (1,0) 0 071(1,0) X y=log x
导航 课前·基础认知 1.对数函数y=logax(a>0,且a≠1)的图象与性质 a的取值范围 a>1 0<a<1 图象

导航 的取值范围 a>1 0<<1 函数值 当0<x<1时, 当0<x<1时, 性 的变化 当x>1时, 当x>1时, 质 在区间0,+o)内是 在区间(0,+∞)内是 单调性
导航 a的取值范围 a>1 0<a<1 性 质 函数值 的变化 当0<x<1时, y<0 当x>1时, y>0 当0<x<1时, y>0 当x>1时, y<0 单调性 在区间(0,+∞)内是 增函数 在区间(0,+∞)内是 减函数

导航 2.反函数 般地,指数函数y=(>0,且呋1)与对数函数y=logx(>0,且 呋1)互为 ,它们的定义域与值域正好 微拓展并不是任何一个函数y=f),都有反函数只有定义域 和值域满足一一对应的函数才有反函数
导航 2.反函数 一般地,指数函数y=ax (a>0,且a≠1)与对数函数y=logax(a>0,且 a≠1)互为 反函数 ,它们的定义域与值域正好 互换 . 微拓展 并不是任何一个函数y=f(x),都有反函数.只有定义域 和值域满足一一对应的函数才有反函数