
全程设计 第四章 指数丞数与对数函数 4.5 函数的应用(二) 4.5.1 函数的零点与方程的解
第四章 指数函数与对数函数 4.5 函数的应用(二) 4.5.1 函数的零点与方程的解

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
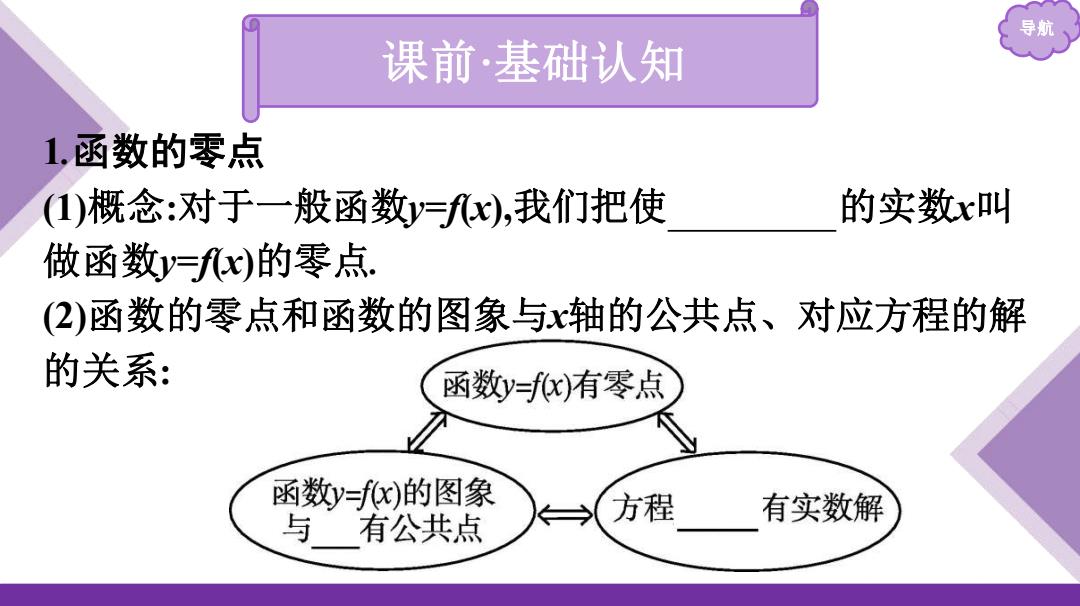
导航 课前·基础认知 1,函数的零点 (1)概念:对于一般函数y=fx),我们把使 的实数x叫 做函数y=f)的零点 (2)函数的零点和函数的图象与x轴的公共点、对应方程的解 的关系: 函数y=fx)有零点 函数y=x)的图象 与有公共点 →(方程 有实数解
导航 课前·基础认知 1.函数的零点 (1)概念:对于一般函数y=f(x),我们把使 f(x)=0 的实数x叫 做函数y=f(x)的零点. (2)函数的零点和函数的图象与x轴的公共点、对应方程的解 的关系:

导航 微点拨1(1)函数的零点不是一个点,而是一个实数,当自变量 取该实数时,函数值为零; (2)并不是任何函数都有零点,比如y=1y=x2+1等就没有零点; (3)若函数x)有零点,则零,点一定是定义域内的一个实数
导航 微点拨1 (1)函数的零点不是一个点,而是一个实数,当自变量 取该实数时,函数值为零; (2)并不是任何函数都有零点,比如y=1,y=x2+1等就没有零点; (3)若函数f(x)有零点,则零点一定是定义域内的一个实数
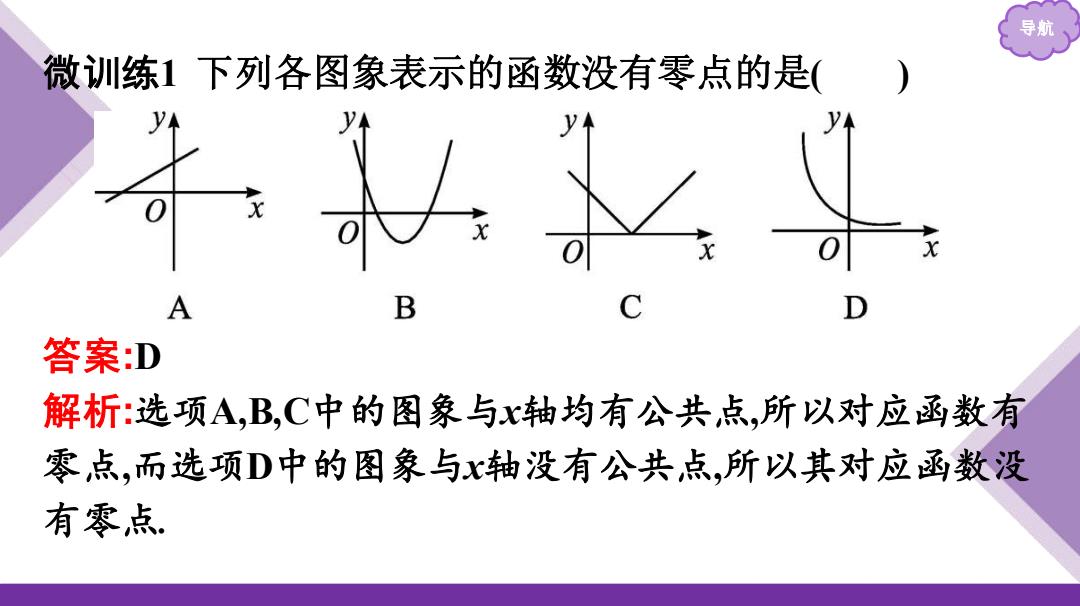
导期 微训练1下列各图象表示的函数没有零点的是( A B 答案:D 解析:选项A,B,C中的图象与x轴均有公共点,所以对应函数有 零点,而选项D中的图象与x轴没有公共点,所以其对应函数没 有零点
导航 微训练1 下列各图象表示的函数没有零点的是( ) 答案:D 解析:选项A,B,C中的图象与x轴均有公共点,所以对应函数有 零点,而选项D中的图象与x轴没有公共点,所以其对应函数没 有零点