导航 微判断 (1)半角公式适用于任意角. (×) 1-C0s30° (2)sin15°=±、 2 (X) (3)c0s = 1+C0S0 2 (X (4)若角a是第一象限角,则ta吃 1-cosa = \1+cosa
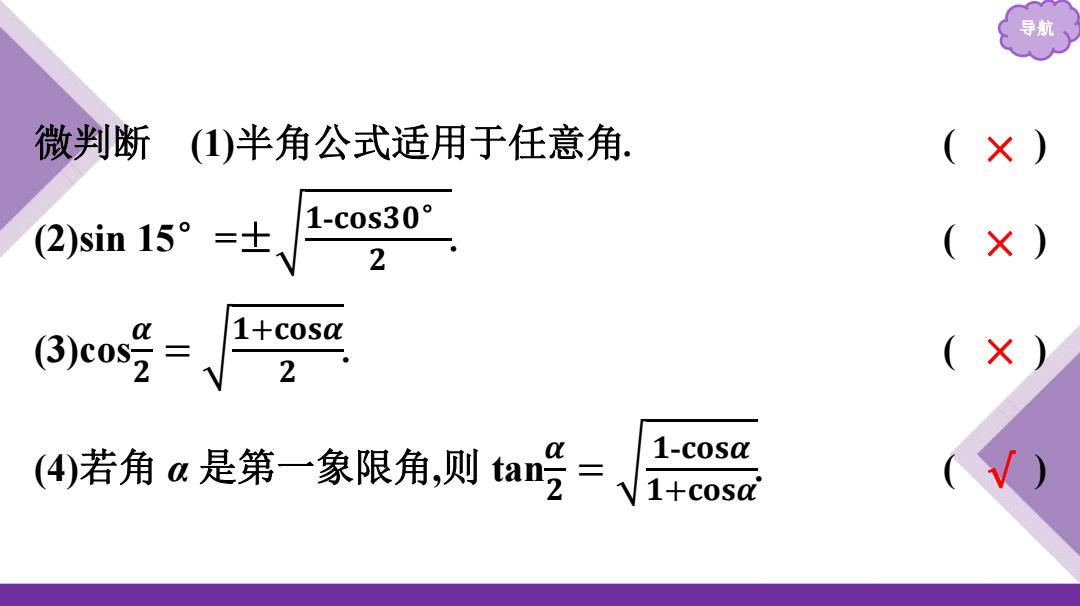
导航 微判断 (1)半角公式适用于任意角. ( ) (2)sin 15°=± 𝟏-𝐜𝐨𝐬𝟑𝟎° 𝟐 . ( ) (3)cos𝜶 𝟐 = 𝟏+𝐜𝐨𝐬𝜶 𝟐 . ( ) (4)若角 α 是第一象限角,则 tan𝜶 𝟐 = 𝟏-𝐜𝐨𝐬𝜶 𝟏+𝐜𝐨𝐬𝜶 . ( ) × × × √

导航 微训练已知cosu号a∈(受,2m,则a等于 答案号 解析:ra∈(z,2m)∈(m 4 又c0suF 4 1-c0S0 1 4 1十 3
导航 微训练 已知 cos α= 𝟒 𝟓 ,α∈ 𝟑𝛑 𝟐 ,𝟐𝛑 ,则 tan𝜶 𝟐 等于 . 答案:- 𝟏 𝟑 解析:∵α∈ 𝟑𝛑 𝟐 ,𝟐𝛑 ,∴ 𝜶 𝟐 ∈ 𝟑𝛑 𝟒 ,𝛑 . 又 cos α= 𝟒 𝟓 , ∴tan𝜶 𝟐 =- 𝟏-𝐜𝐨𝐬𝜶 𝟏+𝐜𝐨𝐬𝜶 =- 𝟏- 𝟒 𝟓 𝟏+ 𝟒 𝟓 =- 𝟏 𝟑

导航 课堂·重难突破 利用半角公式求值 典例剖析 1.(诺sin0-g,53元则sin号 (2已知cos0石0∈(r2m,则sinteo号一 答案0)3 (2明
导航 课堂·重难突破 一 利用半角公式求值 典例剖析 1.(1)若 sin θ= 𝟑 𝟓 , 𝟓𝛑 𝟐 <θ<3π,则 sin𝜽 𝟐 = . (2)已知 cos θ=- 𝟕 𝟐𝟓 ,θ∈(π,2π),则 sin𝜽 𝟐 +cos 𝜽 𝟐 = . 答案:(1)- 𝟑√𝟏𝟎 𝟏𝟎 (2)𝟏 𝟓