
全程设计 第四章 指数数与对数数 4.4对数函数 第3课时 不同函数的增长差异
第四章 指数函数与对数函数 4.4 对数函数 第3课时 不同函数的增长差异

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
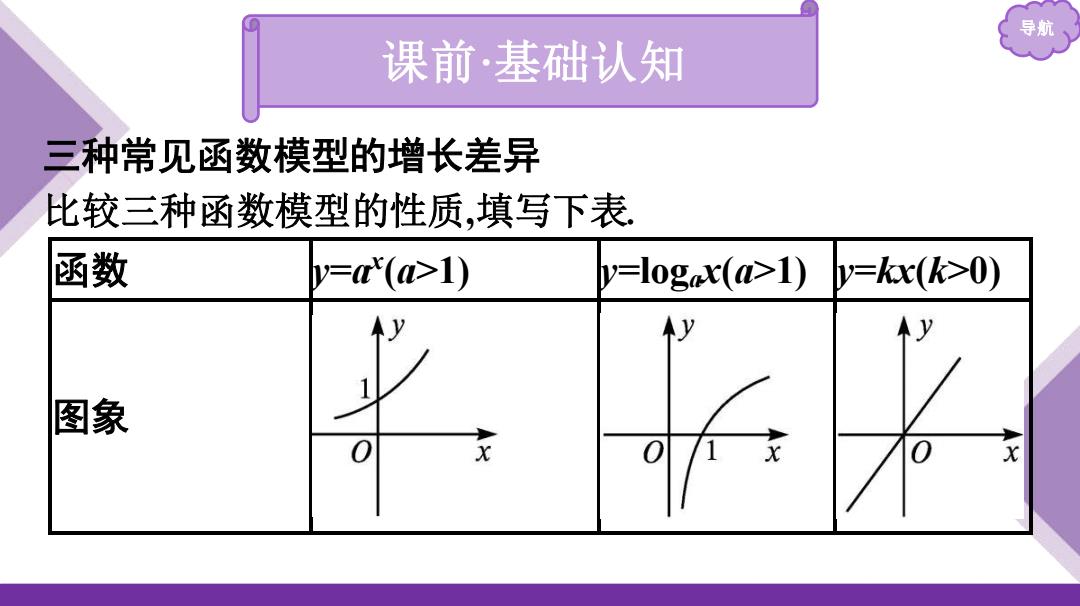
导航 课前·基础认知 三种常见函数模型的增长差异 比较三种函数模型的性质,填写下表 函数 ='(a>1) y=logax(a>1)y=kx(k>0) y y 1 图象 0 0
导航 课前·基础认知 三种常见函数模型的增长差异 比较三种函数模型的性质,填写下表. 函数 y=ax (a>1) y=logax(a>1) y=kx(k>0) 图象

导航 函数 y=(a>1) v=log x(a>1) y=kx(k>0) 在区间(0,+oo) 内的单调性 随x的增大逐渐变 随x的增大逐渐 图象的变化 直线上升 “陡” 趋于平缓 的增长 增长速度 kcx的增长;logx的增长慢 于x的增长 增长后果 存在一个xo,当x>x时,恒有
导航 函数 y=ax (a>1) y=logax(a>1) y=kx(k>0) 在区间(0,+∞) 内的单调性 单调递增 单调递增 单调递增 图象的变化 随x的增大逐渐变 “陡” 随x的增大逐渐 趋于平缓 直线上升 增长速度 a x的增长 大大超过 kx的增长;logax的增长慢 于kx的增长 增长后果 存在一个x0 ,当x>x0时,恒有 a x>kx>logax

微判断()当x每增加一个单位时,y增加或减少的量为定值, 则是x的一次函数.(√) (2)函数y=log2x增长的速度越来越慢(√) (3)不存在一个实数m,使得当x>m时,1.1>100x(× 解析:()因为一次函数的图象是一条直线,所以当x增加一个 单位时y增加或减少的量为定值 (2)由函数y=l0g2x的图象(图略)可知其增长的速度越来越慢, (3)根据指数函数和一次函数增长速度的比较可知存在一个 实数m,使得当x>m时,1.1>100x
导航 微判断 (1)当x每增加一个单位时,y增加或减少的量为定值, 则y是x的一次函数.( ) (2)函数y=log2x增长的速度越来越慢.( ) (3)不存在一个实数m,使得当x>m时,1.1 x>100x.( ) 解析:(1)因为一次函数的图象是一条直线,所以当x增加一个 单位时,y增加或减少的量为定值. (2)由函数y=log2x的图象(图略)可知其增长的速度越来越慢. (3)根据指数函数和一次函数增长速度的比较可知存在一个 实数m,使得当x>m时,1.1 x>100x. √ √ ×