《高等数学》课程教学资源（PPT课件）第十章 重积分 10-04 第四节 重积分的应用

曲面的面积设光滑曲面S:z=f(x,y),(x,y)ED则面积A可看成曲面上各点M(x,y,z)处小切平面的面积dA无限积累而成设它在D上的投影为则Xdo, do =cosy.dA1ncosY1+ f2(x,y)+ f,(x,y)M1do

 M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积A可看成曲面上各点 M x y z ( , , ) 处小切平面的面积dA无限积累而成. 设它在D上的投影为 d, d = cos d A 2 2 1 cos 1 ( , ) ( , ) x y f x y f x y  = + + 则   M n  d

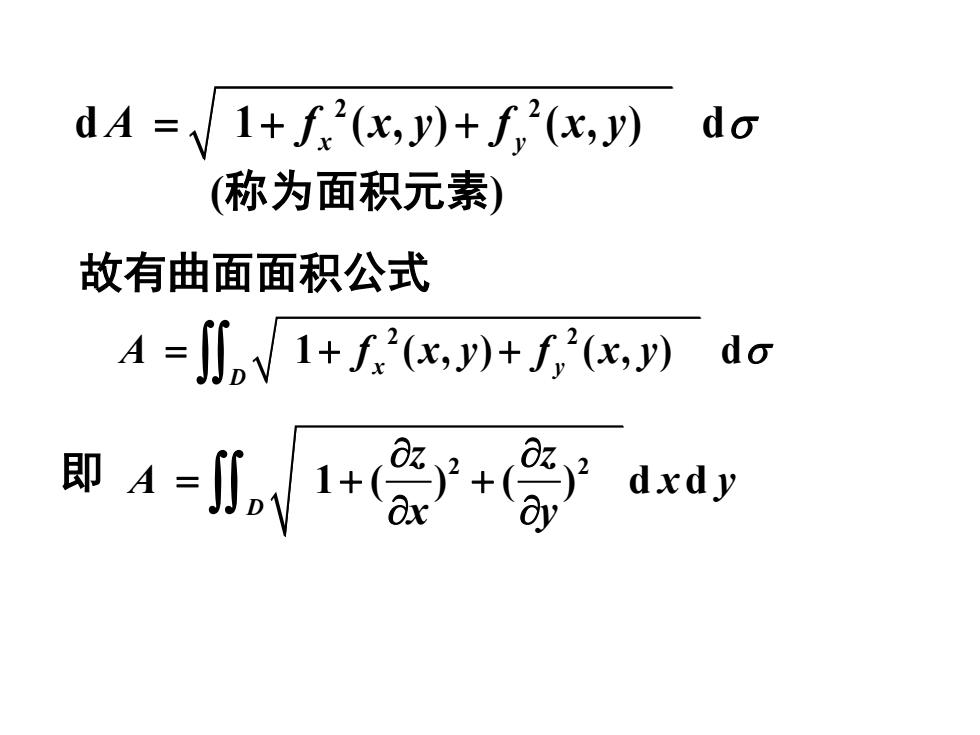
dgdA =/ 1+ f(x,J)+ f?(x,y)(称为面积元素)故有曲面面积公式A = [J, 1+ f?(x,y)+ f,'(x,y)dgOz.Oz.即 A=J,1dxdydxd

故有曲面面积公式 2 2 1 ( , ) ( , ) d x y D A f x y f x y = + +   2 2 1 ( ) ( ) d d D z z A x y x y   = + +   即  2 2 d 1 ( , ) ( , ) d A f x y f x y = + + x y  (称为面积元素)

若光滑曲面方程为x=g(y,z)，(y,z)eD则有axax)2dydz1+(ayazD若光滑曲面方程为 y=h(z,x)，(z,x)eD,x则有ayay>2dzdx1+azax

2 2 1 ( ) ( ) d d y y A z x z x   = + +    若光滑曲面方程为 ( , ) , ( , ) , z x y h z x z x D =  则有 D z x 若光滑曲面方程为 ( , ) , ( , ) , y z x g y z y z D =  则有 D y z

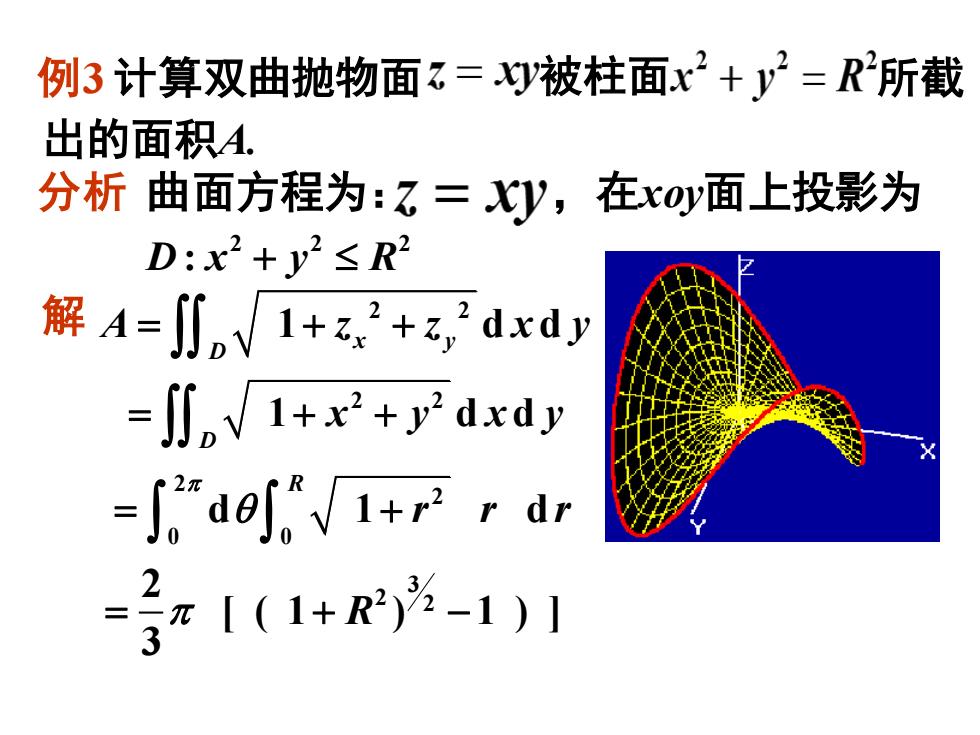
例3计算双曲抛物面=xy被柱面x2+y2=R"所截出的面积A.分析日曲面方程为：z=XV，在xoy面上投影为D:x? + y?≤R?解 A=J,1+z?+z, dxdy=JJ,1+x +y?dxdy2元de/ 1+r2 r dr2[(1+R’)%-1) ]元3

例3 计算双曲抛物面 被柱面 所截 分析 曲面方程为： ，在xoy面上投影为 2 2 1 d d x y D A z z x y = + +  2 2 1 d d D = + + x y x y 2 2 0 0 d 1 d R r r r  = +    3 2 2 2 [ ( 1 ) 1 ) ] 3 = + −  R 出的面积A. 解 2 2 2 D x y R : + 

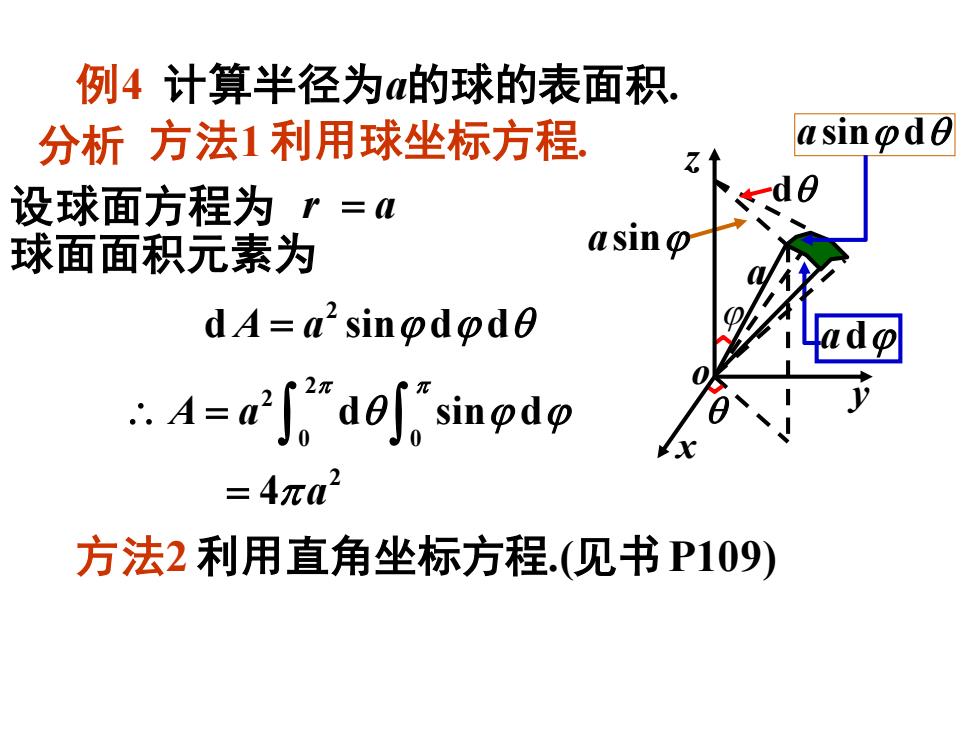
例4i计算半径为的球的表面积asin@de方法1利用球坐标方程分析7.de设球面方程为r=aasing球面面积元素为dA= a’ sinpdpdeadp27y1"del"singdpA== 4元a2方法2利用直角坐标方程.（见书P109)

例4 计算半径为a的球的表面积. 分析 设球面方程为 r a = 球面面积元素为 2 d sin d d A a =    2 2 0 0 A a d sin d    =      2 = 4a asin ad 方法2 利用直角坐标方程.(见书P109) 方法1 利用球坐标方程.   a x y z o d asin d  