
复变函数2.映射的定义:如果用Z平面上的点表示自变量的值而用另一个平面w平面上的点表示函数w的值,那末函数w=f(z)在几何上就可以看作是把z平面上的一个点集G(定义集合)变到W平面上的一个点集G*(函数值集合)的映射(或变换)。U
6 2.映射的定义: ( ). * ( ) ( ) , ( ) , 或变换 平面上的一个点集 函数值集合 的映射 是 把 平面上的一个点集 定义集合 变 到 值 那末函数 在几何上就可以看作 而用另一个平面 平面上的点表示函数 的 如果用 平面上的点表示自变量 的 值 w G z G w f z w w z z =

复变函数这个映射通常简称为由函数w= f(z)所构成的映射如果G中的点z被映射w= f(z)映射成G*中的点w,那末w称为z的象(映象),而z称为w的原象U
7 . , ( ), ( ) * 的原象 中的点 那 末 称 为 的 象 映 象 而 称 为 如 果 中的点 被映射 映射成 w w z z w G z w = f z G . ( ) 所构成的映射 这个映射通常简称为由函 数 w = f z
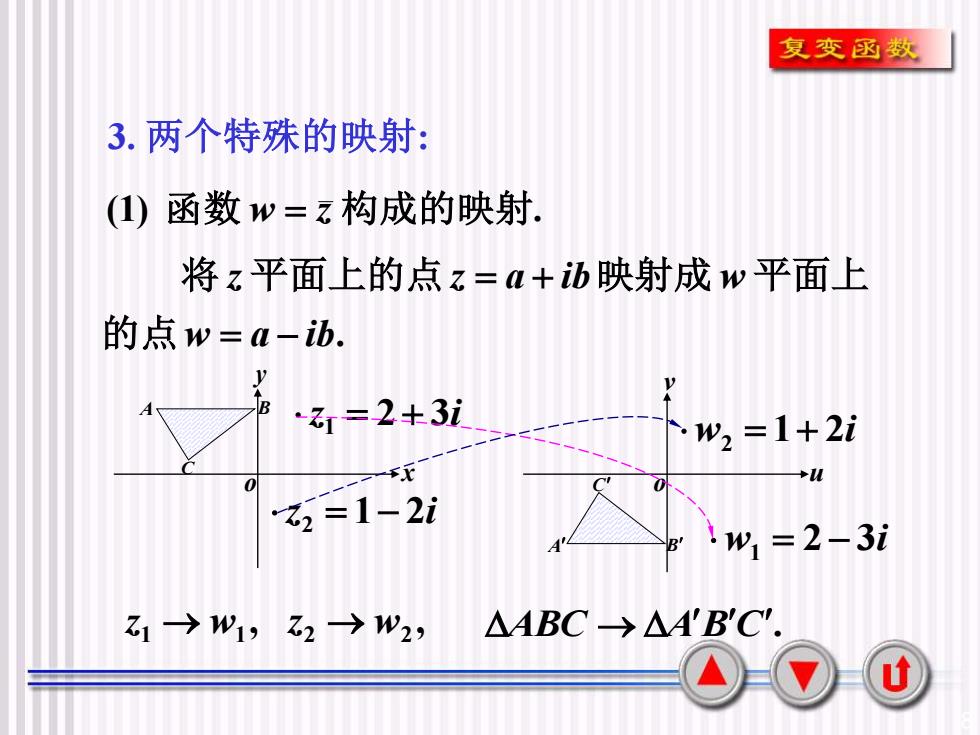
复变函数3.两个特殊的映射:(1)函数W=z构成的映射将z平面上的点z=a+映射成w平面上的点w=a-ib.YB-=2+3i.w2 =1+2i4x+u =1-2i!Wi =2-3i△ABC-AA'B'C'Zi →W1,Z2 →W2,U
8 (1) 函数 w = z 构成的映射. x y o u v o z 2 3i 1 = + w 2 3i 1 = − z 1 2i 2 = − w 1 2i 2 = + A B C A B C , 1 w1 z → , 2 w2 z → ABC → ABC . 3. 两个特殊的映射: . w a ib z z a ib w = − = + 的点 将 平面上的点 映射成 平面上