第四节函数的单调性与曲线的凹凸性 例1判定函数y=x-sinx在0,2π上的单调性. 解 y=x-sin x 2π 上页 下页 返回 MathGS 公式 线与面 数学家
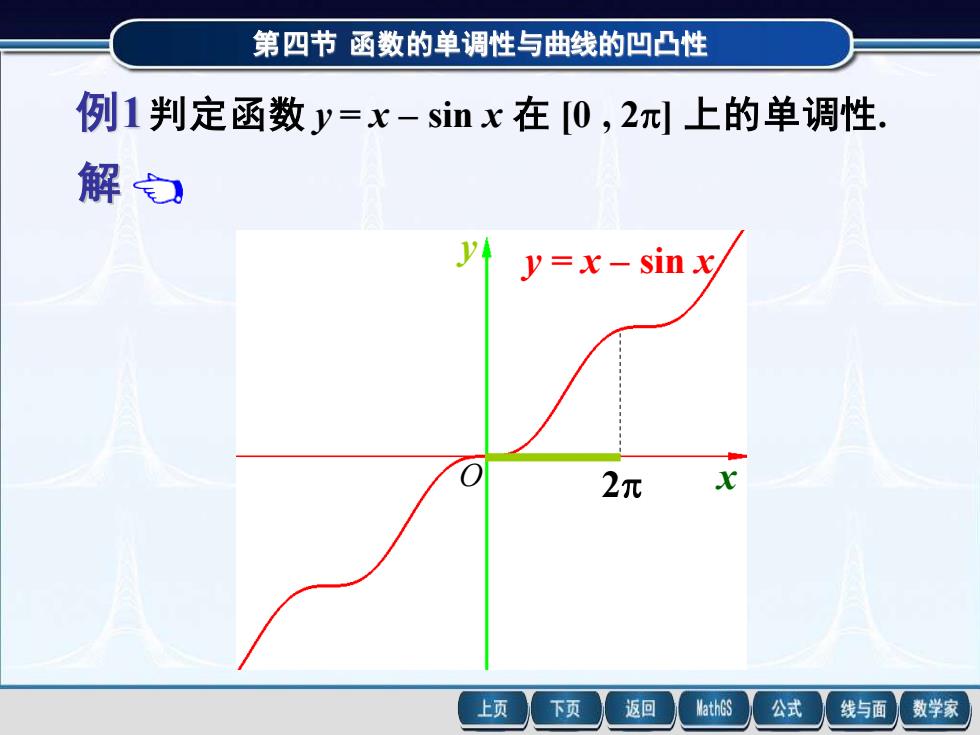
第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 例1 判定函数 y = x – sin x 在 [0 , 2] 上的单调性. 因为在 (0 , 2) 内 y = 1 – cos x > 0 , 所以函数 y = x – sin x 在 [0 , 2] 上的单调增加. 事实上该函数在整个 定义域 (- , + ) 上都是 单调增加的. 2 y = x – sin x x y O 例1 判定函数 y = x – sin x 在 [0 , 2] 上的单调性. 2 y = x – sin x x y O
第四节函数的单调性与曲线的凹凸性 例2讨论函数y=ex-x-1的单调性. 解 、y=er-x-1 上页 下页 返回 MathGS 公式 线与面 数学家
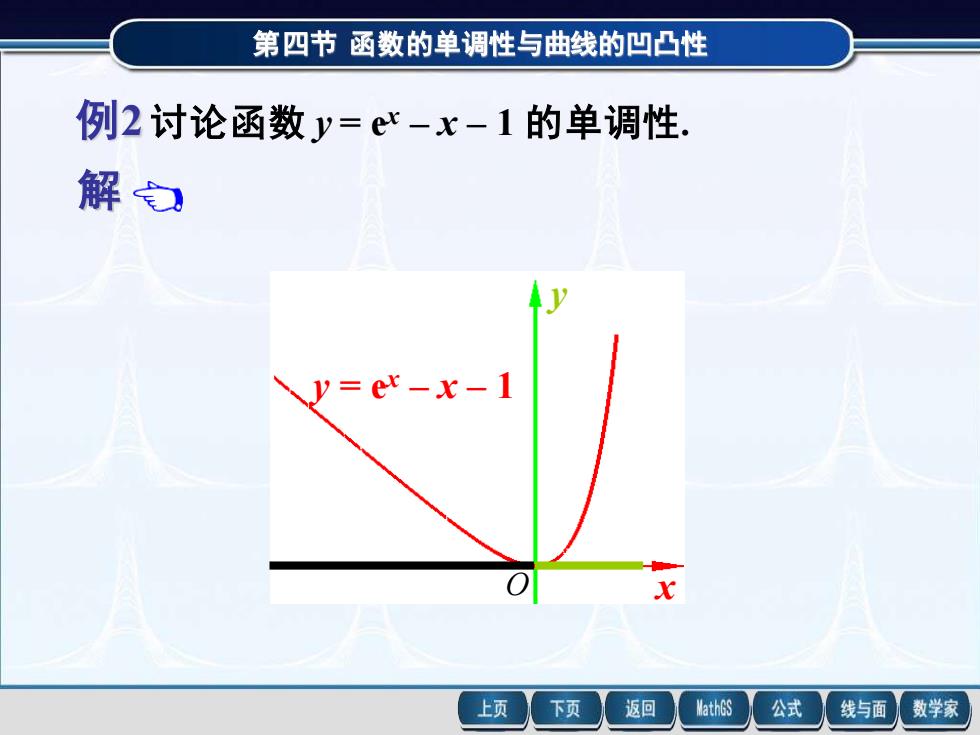
第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 例2 讨论函数 y = ex – x – 1 的单调性. 函数的定义域为 (- , + ) . y = ex – 1 , 当 x < 0 时,y < 0,所以函数 y = ex – x – 1 在 (- , 0] 上单调 减少; 当 x > 0 时,y > 0,所以函数 y = ex – x – 1 在 [0 , + ) 上单调增加. y = ex – x – 1 x y O 例2 讨论函数 y = ex – x – 1 的单调性. y = ex – x – 1 x y O
第四节函数的单调性与曲线的凹凸性 例3讨论函数y=Vx2的单调性. 解 y=Vx 上页 下页 返回 MathS 公式 线与面 数学家
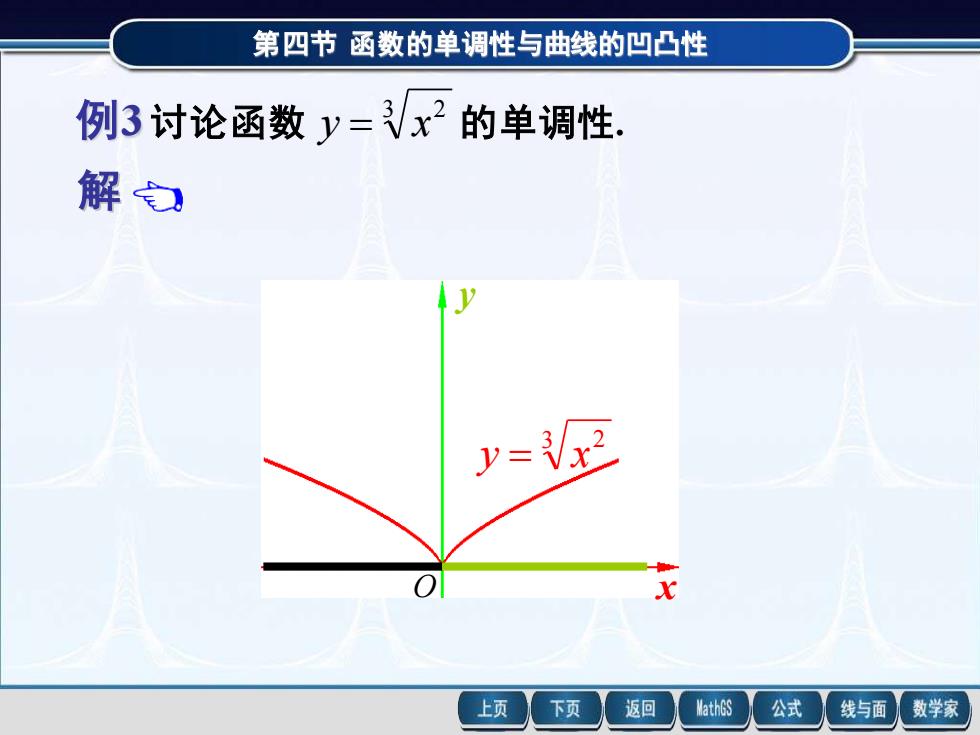
第四节 第四节 函数的单调性与曲线的凹凸性 函数的单调性与曲线的凹凸性 解 函数的定义域为 (- , + ) . 当 x < 0 时,y < 0,所以函数 在 (- , 0] 上单调减少; 当 x > 0 时,y > 0,所以函数 在 [0 , + ) 上单调增加. 例3 讨论函数 3 2 y = x 的单调性. , 3 2 3 x y = 当 x = 0 时,y 不存在. 3 2 y = x x y O 例3 讨论函数 3 2 y = x 的单调性. 3 2 y = x x y O