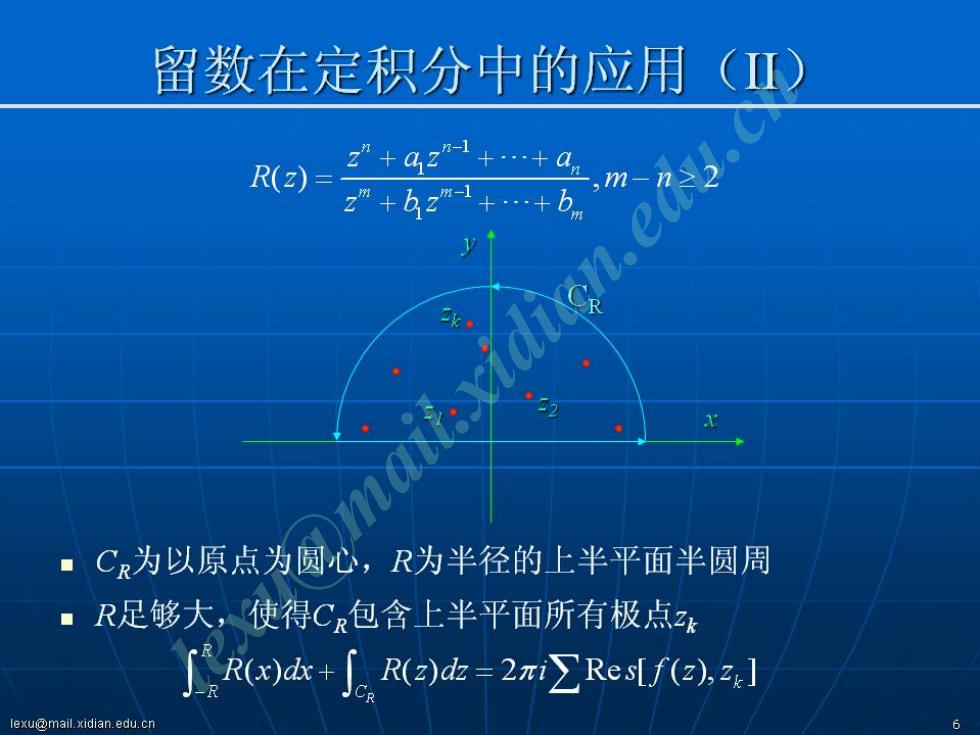
留数在定积分中的应用(Ⅱ) R(z)= z”+42++a2 z"+bzm1+…+b C为以原点为圆心,R为半径的上半平面半圆周 R足够大,使得C包含上半平面所有极点zk R(x)de+R(2)d:-2riReslf(2),z1 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

留数在定积分中的应用(Ⅱ) R(2)= 111+4z1++a,2”1 1 1+az+...+az zm-"1+么z1+…+bz"11zm1b21++bn2m bz1+…+五2m 当足够大时 z1+. +a,z"10 IR水品 作R足够大的CR上 R im R(ad0 R(x)k=2∑Refa),] 若R)为偶函数 6 R(x)d&=πi∑Res[f(z),z] lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

留数在定积分中的应用() 例1计算积分:1= x"dx (+a2e+ba>0b>0 ·[解]易验证 ·积分函数是x的有理函数 162 a b 2i(a2-b)2ib2-a2) mm=4,n=2,m-n=2 函数的奇点为士ai,◆士bi,不在实轴上 a+b ·利用积分类型Ⅱ采用留数求解,显然,在上半平面仅有 级极点a1,bi,且它们的留数为: Res[R(Z).ai-lim[(-aI)R()- -q2 a 2ai(b"-a') 2i(a2-b2) -b2 b Res[R(2).bi]=lim [(z-bi)R(2)]= 2bi(a2-b22i62-a2) lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

留数在定积分中的应用( 积分类型m:「eeo>)d ·R(x)是x的有理函数 。分母的次数至少比分子的次数高一次 。在实轴上没有孤立奇点 ·同样,不失一般性,设 R(2) 2”+1z1 ++a,m-n21 exu z"+bz"-++b lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

留数在定积分中的应用(Ⅱ) 111+gz1+…+a,2” 1la21++a,2 zm-m1+bz+…+bz"1|zm-11z1+…+bn2 bz+…+b 当足够大时 q2+ 10 在R足够大的CR上 Ro 2 imR(e"d=0 lexu@mail.xidian.edu.cn 10
lexu@mail.xidian.edu.cn