
二、函数概念 1.有关的概念 2.函数的表示法 (1)设x和y是两个变量,D是一个数集. 如果对 (1)表格法 于D中的每一个x,按照某照某个对应法则∫,变量 (2)图形法 y都有唯一确定的值和它对应,那么称对应法则∫为 (3)解析法 定义在数集D上的函数.数集D叫做函数的定义域 x叫做自变量,y叫做因变量. 注记1:记号∫与f(x)的含义不同. 注记3:求函数的定义域的方法: 记号∫表示自变量与因变量之间的函数关系 (1)根据实际意义确定 记号(x)表示自变量对应的函数值. (2)根据解析式确定 为了方便,常用记号f(x)或y=f(x)表示函数. 注记2:函数的两个要素:对应法则、定义域. 2)在定义域的不同部分,对应法则不同的函数称为 分段函数
二、函数概念 1. 有关的概念 2. 函数的表示法 ( 1) 设 x 和 y 是两个变量, D 是一个数集. 如果对 于 D 中的每一个 x ,按照某照某个对应法则 f ,变量 注记 1:记号 f 与 f ( ) x 的含义不同. x叫做自变量, y 叫做因变量. y 都有唯一确定的值和它对应,那么称对应法则 f 为 定义在数集 D 上的函数. 数集 D 叫做函数的定义域. 记号 f 表示 自变量与因变量之间的函数关系. 记号 f ( ) x 表示 自变量对应的函数值. 为了方便,常用记号 f ( ) x 或 y fx = ( ) 表示函数. 注记 2:函数的两个要素:对应法则、定义域. (2)在定义域的不同部分,对应法则不同的函数称为 分段函数 (1)表格法 (2)图形法 (3)解析法 注记 3:求函数的定义域的方法: ( 1 )根据实际意义确定 (2) 根据解析式确定

二、函数的概念 3.常见的几种特殊函数 3.常见的几种特殊函数 (1)常数函数:y=C,C为常数 当C≠0时,它的图形是一条平行于x轴的直线 定义域D=(-0,+o),值域W={C 当C=0时,它的图形就是x轴 (2)绝对值函数y== x≥0 -xx<0 定义域D=(-0,+o0),值域W=[0,+oo). 1 当x>0 (3)符号函数y=sgnx= 0 当x=0 定义域D=(-0,+∞),值域W={-1,0,} -1 当x<0 (4)取整函数:y=[x]表示不超过x的 定义域D=(-o,+o),值域为整数集Z 最大整数 (5)取最值函数:y=max{f(x),g(x)月 y=min{f(x),g(x))
二、函数的概念 3. 常见的几种特殊函数 3.常见的几种特殊函数 ( 1 )常数函数: y = C, C 为常数 定义域 D = (,) −∞ +∞ ,值域 W C ={ } 当 C ≠ 0时,它的图形是一条平行于 x 轴的直线 当 C = 0时,它的图形就是 x 轴 ( 2 )绝对值函数 0 0 x x y x x x ⎧ ≥ = = ⎨ ⎩− < 定义域 D = −∞ +∞ (,),值域 W = [0, ) +∞ . ( 3 )符号函数 1 0 sgn 0 0 1 0 当 当 当 x yx x x ⎧ > ⎪ == = ⎨ ⎪− < ⎩ 定义域 D = −∞ +∞ (,),值域 W = {-1,0,1} ( 4 )取整函数: y = [ ] x 表示不超过 x 的 最大整数 定义域 D = −∞ +∞ (,),值域为整数集 Z (5)取最值函数: y f x gx = max{ ( ), ( )} y = min { f x gx ( ), ( ) }
二、函数的概念 0 →x 4-329 L11234
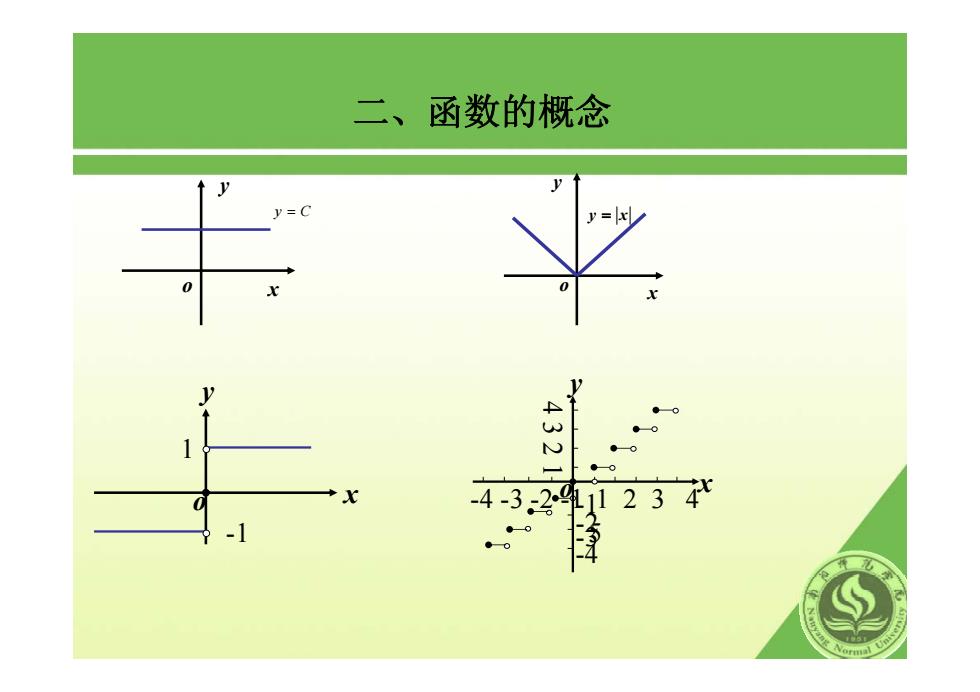
x y o y C = y = x x y o 1 -1 x y o 1 2 3 4 5 -2 -4 -4 -3 -2 -1 4 3 2 1 -1 -3 x y o 二、函数的概念

三、函数的特性 1.函数的单调性 单调递增 单调递减 设函数y=fx)的定义域为D,区间IcD.如果对于区间I上 任意两点x,x,当x<x,时恒有 f(x)<f(x2) f(x)>f(x2) 称函数fx)在区间I上是单调递增. 称函数f)在区间I上是单调递减 y=f(x) v=f (x) I f(x (xI f(x 0 0
三、函数的特性 1.函数的单调性 单调递增 单调递减 设函数 y = f(x )的定义域为 D, 区间 I ⊂D. 如果对于区间 I 上 任意两点 1 2 x x, , 当 1 2 x < x 时恒有 ( ) ( ) 1 2 f x < f x 称函数 f(x )在区间 I 上是单调递增. 1 2 f () ( ) x fx > 称函数 f(x )在区间 I 上是单调递减. x y = f ( x ) ( ) 1 f x ( ) 2 f x x y o I y = f ( x ) ( ) 1 f x ( ) 2 f x x y o I

三、函数的特性 2.函数的有界性 设函数的定义域为D,数集xcD如果存在 设函数的定义域为D,数集 正数M,使对任一xeX有 XcD.对任何M总存在reX使 f(x)≤M f(x)≥M lf(x)≤M Lfx)>M. 称在X上有称在X上有 上界.M为下界.M为) 称在X上有界 称在x上无界 在x上的一个 在x上的一个 上界 下界 函数在x上有界的充要条 件是函数在x上既有上界 f 又有下界 有界0 -M
三、函数的特性 x 2.函数的有界性 设函数 f(x)的定义域为 D, 数集 X⊂ D. 如果存在 正数 M , 使对任一 x ∈ X, 有 f ( ) x ≤ M 称 f(x)在 X上有 上界. M 为 f(x) 在 X上的一个 上界. f ( ) x ≥ M 称 f(x)在 X上有 下界. M 为 f(x) 在 X上的一个 下界. f x( ) ≤ M 称 f(x)在 X 上有界. 设函数 f(x)的定义域为 D, 数集 X⊂ D.对任何 M, 总存在 x ∈ X, 使 | f(x) | > M. 称 f(x)在 X 上无界. 函数 f(x)在 X 上有界的充要条 件是函数 f(x)在 X上既有上界 又有下界 M -M y x o y=f(x) X M -M y o x X x0 有界 无界