
区域 冬连续曲线 ·x()、y)为连续实变函数 ·光滑曲线:x'、y)连续,且对于任意t,有 冬简单曲线 [x'(t)]2+[y'(t)]2≠0 ·没有重点的连续曲线称为简单曲线或若尔当曲 线(Jardan) lexu@mail.xidian.edu.cn 矩阵论 6
lexu@mail.xidian.edu.cn 矩 阵 论 6 区域 连续曲线 x(t)、y(t)为连续实变函数 光滑曲线: x’(t)、y’(t)连续,且对于任意t,有 简单曲线 没有重点的连续曲线称为简单曲线或若尔当曲 线(Jardan) 2 2 [ '( )] [ '( )] 0 xt yt + ≠
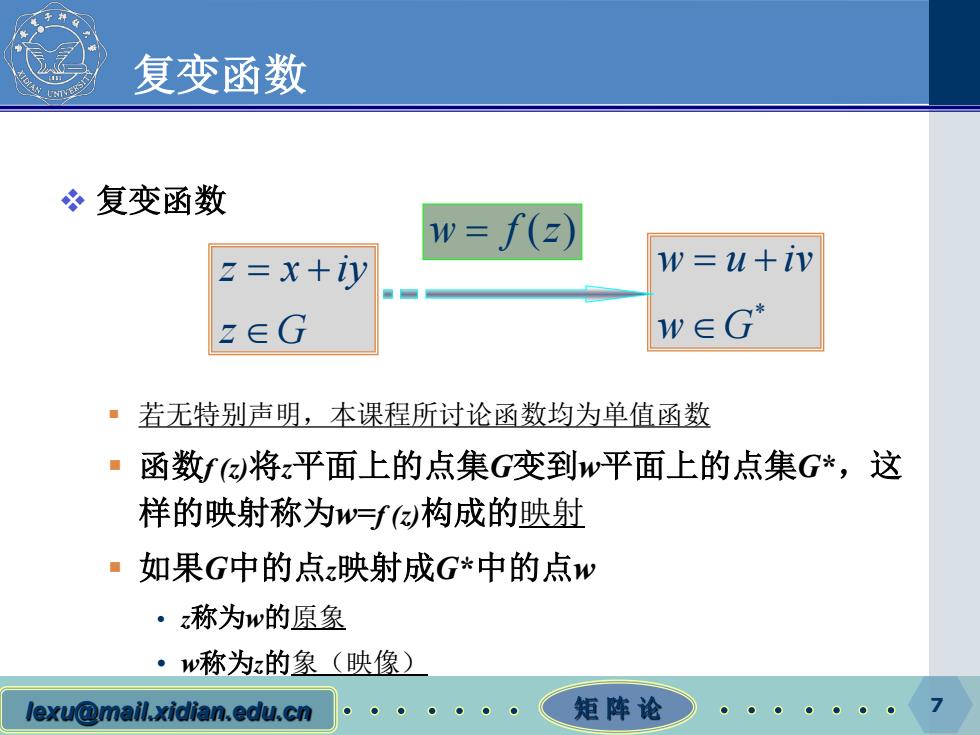
复变函数 冬复变函数 w=f(z) Z=x+iy w=u+iv z∈G w∈G ·若无特别声明,本课程所过论函数均为单值函数 ·函数fa将z平面上的点集G变到w平面上的点集G*,这 样的映射称为w=f亿构成的映射 ·如果G中的点z映射成G*中的点w ·称为w的原象 ·w称为z的象(映像) lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 7 复变函数 复变函数 若无特别声明,本课程所讨论函数均为单值函数 函数f (z)将z平面上的点集G变到w平面上的点集G*,这 样的映射称为w=f (z)构成的映射 如果G中的点z映射成G*中的点w • z称为w的原象 • w称为z的象(映像) w fz = ( ) z x iy z G = + ∈ * w u iv w G = + ∈
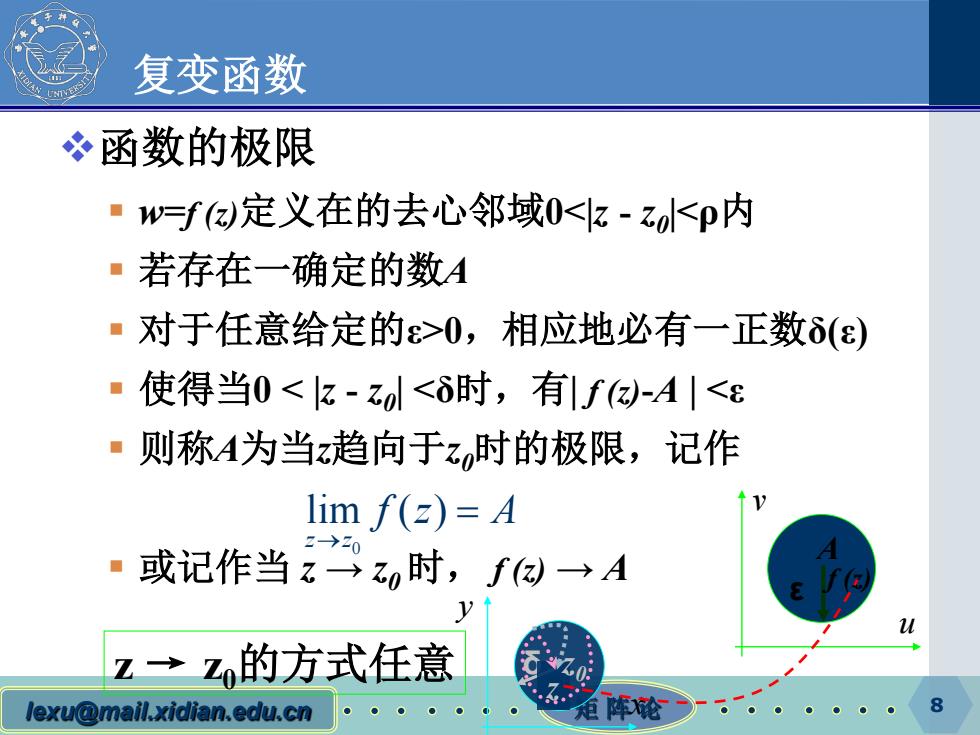
复变函数 冬函数的极限 ·w=f)定义在的去心邻域0<k-z<p内 ·若存在一确定的数A ■对于任意给定的>0,相应地必有一正数δ(ε) ·使得当0<k-z<δ时,有f-A|< ·则称A为当z趋向于z,时的极限,记作 lim f(z)=A ·或记作当z时,f(似→A y 2→Z的方式任意 lexu@mail.xidian.edu.cn 阵轮 8
lexu@mail.xidian.edu.cn 矩 阵 论 8 复变函数 函数的极限 w=f (z)定义在的去心邻域0<|z - z0|<ρ内 若存在一确定的数A 对于任意给定的ε>0,相应地必有一正数δ(ε) 使得当0 < |z - z0| <δ时,有| f (z)-A | <ε 则称A为当z趋向于z0时的极限,记作 或记作当 z → z0 时, f (z) → A 0 lim ( ) z z fz A → = x y u v δ z z0 ε f (z) A z → z0的方式任意

复变函数 函数的连续性 ·若limf(z)=f(z),则f()在zo连续 ·若fa)在区域D内处处连续,则f()在D内连续 ·f(z)=u(x,y)+iv(x,y)在处连续+yo ① u(x,y)与在处连续xo,yo) ·在z连续的两个函数的四则运算在z处仍连续 ·复合函数的连续性质 lexu@mail.xidian.edu.cn 矩阵论 9
lexu@mail.xidian.edu.cn 矩 阵 论 9 复变函数 函数的连续性 若 ,则 f (z) 在 z0 连续 若f (z) 在区域D内处处连续,则 f (z)在D内连续 在z0连续的两个函数的四则运算在z0处仍连续 复合函数的连续性质 0 0 lim ( ) ( ) z z fz fz → = 00 0 0 0 () (, ) (, ) (, ) (, ) ( , ) f z u x y iv x y z x iy uxy vxy x y = + =+ 在处连续 与在处连续

画 解析函数(I) 复变函数的导数 冬复变函数的微分 解析函数 lexu@mail.xidian.edu.cn 矩阵论 。。。。。。。10
lexu@mail.xidian.edu.cn 矩 阵 论 10 解析函数(I) 复变函数的导数 复变函数的微分 解析函数