
i方 s=nxn= 111 =(4,-1,-3) 2-13 故所给直线的对称式方程为一1= 22+2 4-1-3 x=1+4t 参数式方程为y=-t z=-2-3t 解题思路:先找直线上一点;再找直线的方向向量 (自学课本例) 2009年7月3日星期五 6 目录 上页 下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 故所给直线的对称式方程为 参数式方程为 ⎪⎩ ⎪ ⎨ ⎧ −−= −= = + tz ty x t 32 41 = t 4 x − 1 − 1 = y 3 2 − + = z 解题思路 : 先找直线上一点;再找直线的方向向量. = − − )3,1,4( 21 s = × nn 312 111 − = i j k (自学课本 例 1 )

例2求与两平面x-4y=3和2x-y-5z=1的交线平 行且过点(-3,2,5)的直线的方程 解:因为所求在直线与两平面的交线平行,也就是直 线的方向向量s一定同时与两平面的法线向量n1、n2 垂直,所以可以取 s=n×n2=10 -4 =-(47+3j+k) 2-1-5 因此所求直线的方程为 x+3_y-2_2-5 4 3 1 2009年7月3日星期五 7 目录○ 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 例 2 求与两平面 x - 4y = 3 和 2 x - y - 5z = 1 的交线平 行且过点 ( -3, 2, 5)的直线的方程. 解:因为所求在直线与两平面的交线平行,也就是直 线的方向向量s 一定同时与两平面的法线向量 n 1 、 n 2 垂直,所以可以取 1 2 1 0 4 (4 3 ) 215 ijk s = × = − =− + + n n i jk − − G G G G G G 因此所求直线的方程为 325 431 xyz + − − = =

3家定线号-学9平2x+y*:-6的交这 (由课本例3改编) 解:所给直线的参数方程为 x=2+t,y=3+t,2=4+2t, 代入平面方程中,得 2(2+t)+(3+)+(4+2)-6=0 解上列方程,得t=-1.把求得的值代入直线的参数 方程中,即得所求交点的坐标为 x=1,y=2,2=2 2009年7月3日星期五 8 目录 上页下页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 例3 求直线 234 112 xyz − −− = = 与平面 2 x + y + z -6=0的交点. 解:所给直线的参数方程为 x = 2 + t, y =3+ t, z=4+2 t, 代入平面方程中,得 2(2+ t) + (3+ t) + (4+2 t ) -6=0. 解上列方程,得t = -1. 把求得的 t值代入直线的参数 方程中,即得所求交点的坐标为 (由课本例 3改编) x=1, y=2, z=2
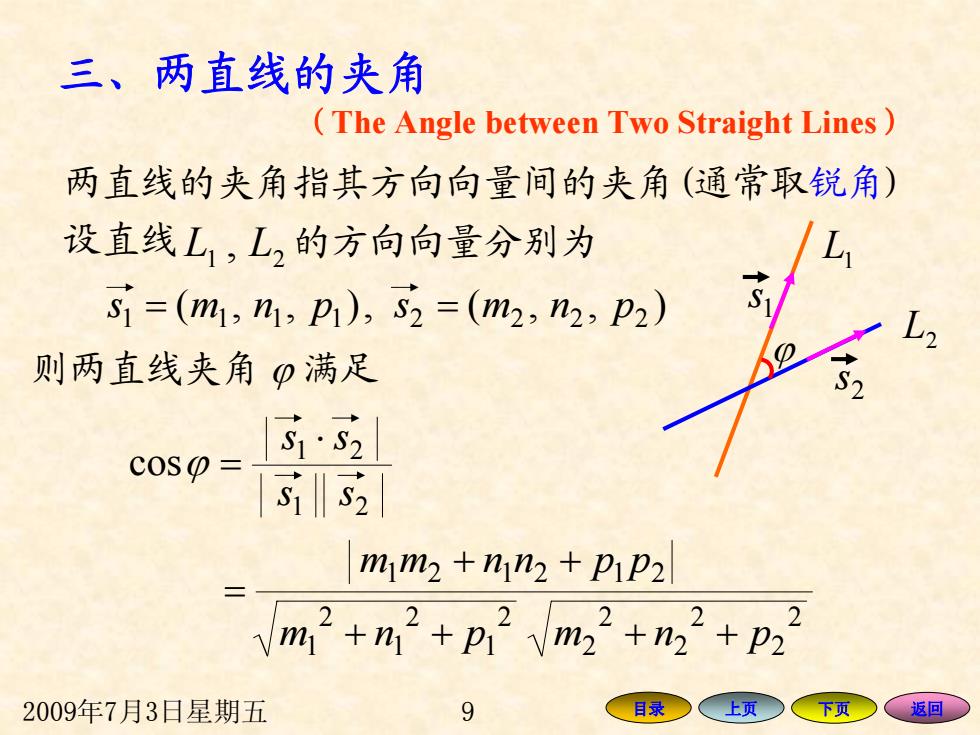
三、两直线的夹角 (The Angle between Two Straight Lines 两直线的夹角指其方向向量间的夹角(通常取锐角) 设直线L,L,的方向向量分别为 S=(m1,n1,P1),S2=(m2,n2,P2) 则两直线夹角0满足 C0S0= 寸·52 s1 mm2+nn2+pip2 Vm2+n2+p2ym22+m22+p2 2 2 2009年7月3日星期五 9 目录○ 上页 下页 、返回
2009年7月3日星期五 9 目录 上页 下页 返回 L 2 L 1 ϕ 则两直线夹角 ϕ 满足 21 设直线 , LL = 两直线的夹角指其方向向量间的夹角(通常取锐角 ) 的方向向量分别为 + + ppnnmm 212121 2 1 2 1 2 1 ++ pnm 2 2 2 2 2 2 ++ pnm ),(,),( 22221111 s = pnm s = pnm 21 21 cos ss s ⋅ s ϕ = 1 s 2 s (The Angle between Two Straight Lines ) 三、两直线的夹角