
例1.求y=3+2x-x2,y=0,x=1, x=4围成的平面图形的面积。 y=3+2x-x y y=3+2x-x1 解 得交点(-1,0),(3,0) y=0 A=1y=3+2x-x2k -1 134 =∫(3+2x-x2-∫3(3+2x-x2x -3x*r-3xrj为 6(?)召面积单位) 8
8 例1.求 2 y x x = + − 3 2 ,y = 0,x =1, x = 4围成的平面图形的面积。 解 2 3 2 0 y x x y = + − = 得交点( 1,0) − ,(3,0) 4 4 2 1 1 A y dx x x dx = = + − | | | 3 2 | 3 4 2 2 1 3 = + − − + − (3 2 ) (3 2 ) x x dx x x dx 2 3 2 3 1 1 3 4 3 3 3 3 1 3 x x x x x x = + − − + − 16 17 23 3 3 3 = − − = (面积单位) −1 o y 1 3 4 x 2 y x x = + − 3 2
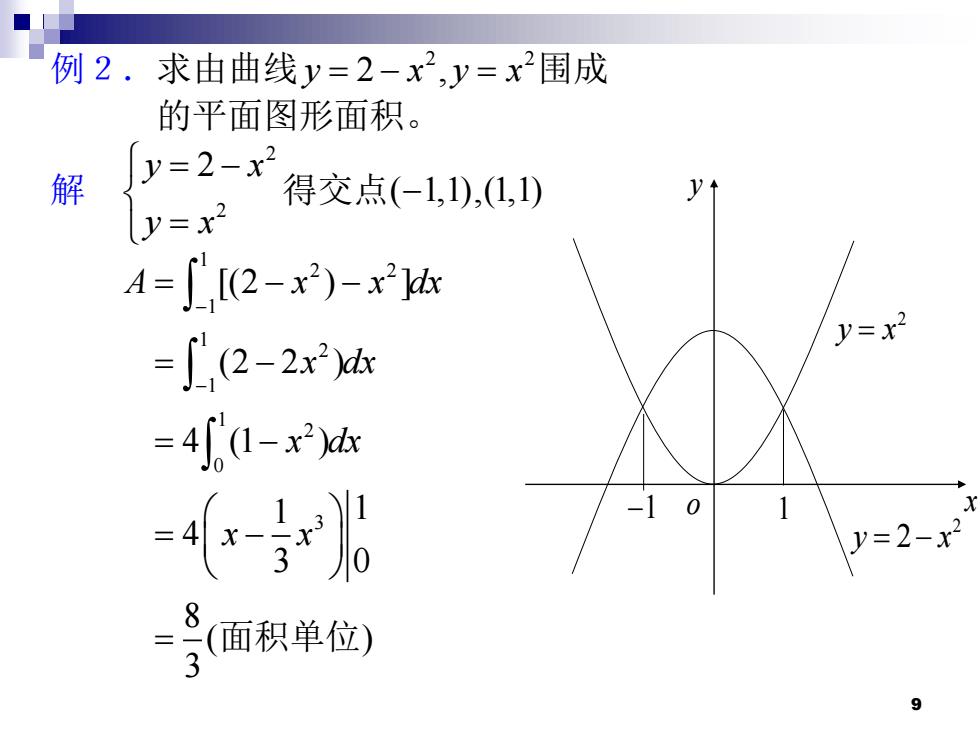
例2.求由曲线y=2-x2,y=x2围成 的平面图形面积。 解 y=2-x 得交点(-1,1),1,1) (y=x2 A=,[(2-x2)-2k y=x2 =∫(2-2x2k =41-x2x =45r8 y=2-x2 8面积华位 9
9 例2.求由曲线 2 y x = −2 , 2 y x = 围成 的平面图形面积。 解 2 2 y x 2 y x = − = 得交点( 1,1) − ,(1,1) 1 2 2 1 1 2 1 1 2 0 3 [(2 ) ] (2 2 ) 4 (1 ) 1 1 4 3 0 8 ( ) 3 A x x dx x dx x dx x x − − = − − = − = − = − = 面积单位 2 y x = −2 y −1 o x 1 2 y x =