
定理2(有界性定理设,f(x) EC[a,b],则f(x)在[a,b]上有界证 设,f(x)EC[a,b],由定理1(最值定理),Vx E[a,b],有m≤f(x)≤M,取 K = max[Iml,I M,则有f(x)≤K:函数f(x)在a,bl上有界
6 证 x [a,b], m f (x) M, max{ }, f (x) K. 函数f (x)在[a,b]上有界. 由定理1(最值定理), 定理2(有界性定理) 有 取 K = | m |,| M | 则有 设 f (x)C[a,b],则f (x)在[a,b]上有界. 设 f (x)C[a,b]
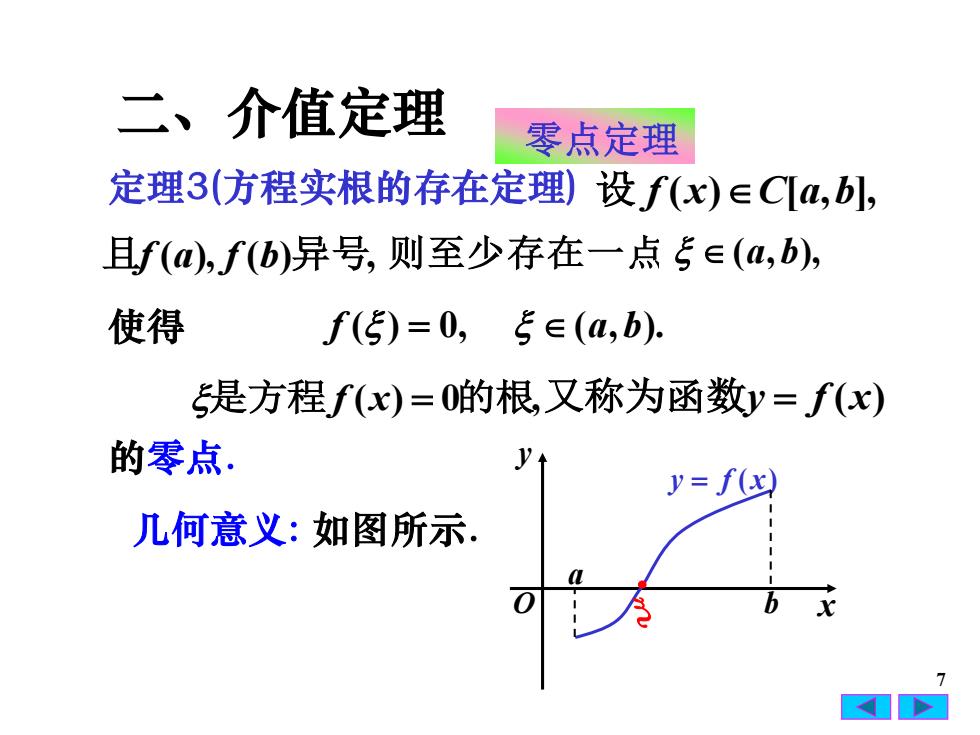
二、介值定理零点定理定理3(方程实根的存在定理)设 f(x) eC[a,b]且f(a),f(b)异号, 则至少存在一点 E (a,b)使得f()=0, e (a,b)是方程f(x)=0的根,又称为函数y= f(x)的零点.yty= f(x)几何意义:如图所示a0bxA
7 的零点. 是方程 f (x) = 0的根,又称为函数y = f (x) 定理3(方程实根的存在定理) 设 f (x)C[a,b], 且f (a), f (b)异号, 则至少存在一点 (a,b), 使得 f ( ) = 0, (a,b). 零点定理 几何意义: 如图所示. 二、介值定理 x y O y = f ( x) b a •