
建立yOz面上曲线C绕z轴旋转所成曲面的方程 给定yOz面上曲线C:f(y,z)=0 若点M1(0,)eC,则有 f(y,)=0 当绕:轴旋转该点转到 M1(0,y1,21) M(x,y,),则有 M(x,y 2=1, x2+y2= 故旋转曲面方程为 f(±x2+y2,)=0 方程的特点:在f(y,)=0中 了不变 y变为士x2+y
建立yOz面上曲线C 绕 z 轴旋转所成曲面的方程: 故旋转曲面方程为 M (x, y,z) , 当绕 z 轴旋转时, ( , ) 0 f y1 z1 (0, , ) , 若点 M1 y1 z1 C 给定 yOz 面上曲线 C: (0, , ) 1 1 1 M y z 1 2 2 1 z z , x y y 则有 ( , ) 0 2 2 f x y z 则有 该点转到 f ( y,z) 0 O z y x C M (x, y,z) 方程的特点:在 f ( y,z) 0 中 z不变 y变为 2 2 x y

思考:当曲线C绕y轴旋转时,方程如何? C:f(y,)=0 f(y,±Vx2+z2)=0
思考:当曲线 C 绕 y 轴旋转时,方程如何? C : f ( y,z) 0 O y x z ( , ) 0 2 2 f y x z
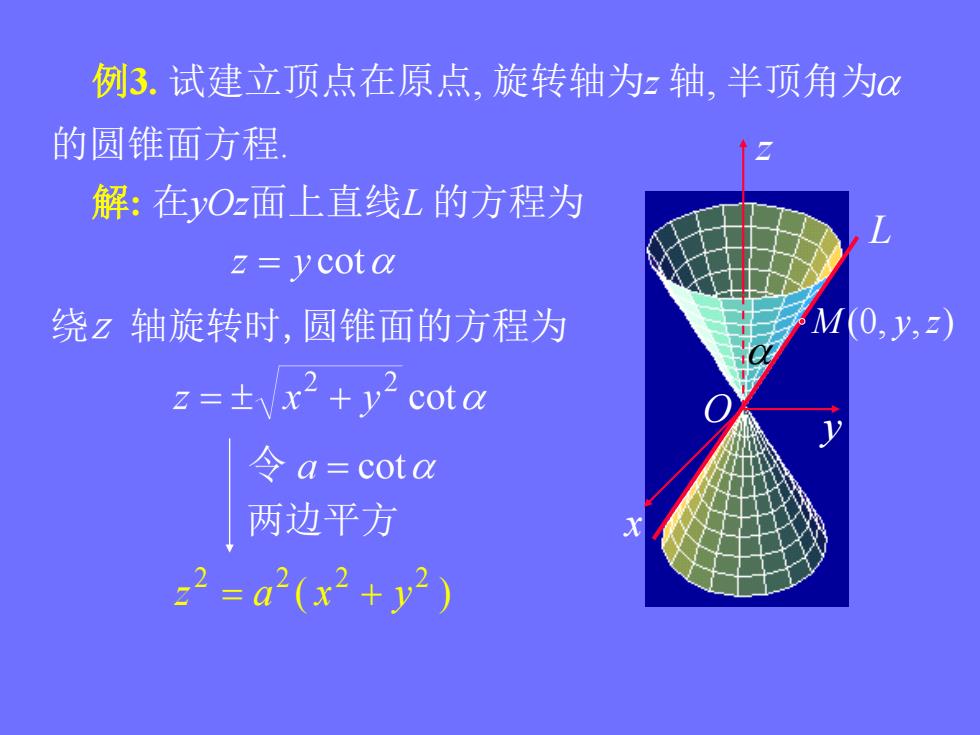
例3.试建立顶点在原点,旋转轴为z轴,半顶角为0 的圆锥面方程 解:在yOz面上直线L的方程为 z=ycota 绕z轴旋转时,圆锥面的方程为 M(0,y,=) z=±x2+y2 cota 令a=cota 两边平方 z2=a2(x2+y2)
x y z O 例3. 试建立顶点在原点, 旋转轴为z 轴, 半顶角为 的圆锥面方程. 解: 在yOz面上直线L 的方程为 绕z 轴旋转时,圆锥面的方程为 ( ) 2 2 2 2 z a x y 两边平方 L M (0, y,z)