
第三章第三节泰勒公式泰勒中值定理一、天二、麦克劳林公式三、泰勒公式的应用HIGH EDUCATION PRESS机动目录上页返回下页结束
二、麦克劳林公式 第三节 一、泰勒中值定理 机动 目录 上页 下页 返回 结束 三、泰勒公式的应用 泰勒公式 第三章
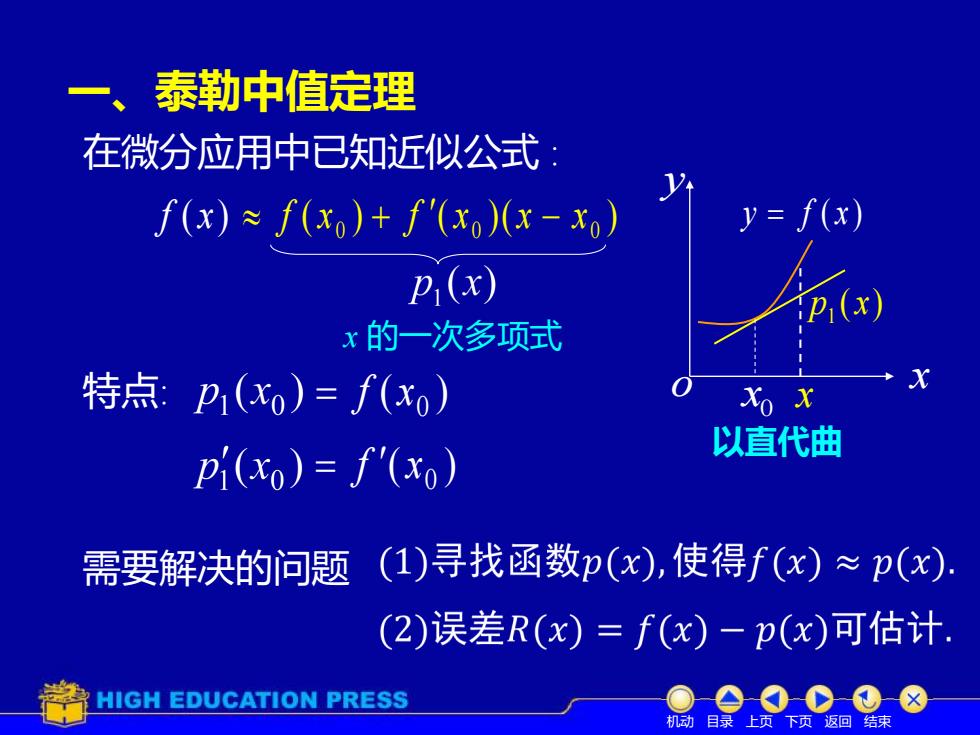
泰勒中值定理一、在微分应用中已知近似公式:y= f(x)f(x) = f(xo)+ f'(xo)(x- xopi(x)(pi(x)x的一次多项式X特点:pi(xo) = f(xo)Xo x以直代曲pi(xo) = f'(xo)(1)寻找函数p(x),使得f(x) ~ p(x)需要解决的问题(2)误差R(x) =f(x)一p(x)可估计HIGH EDUCATION PRESS机动目录上页下页返回结束
特点: ( ) 0 = f x ( ) 0 = f x 一、泰勒中值定理 f ( x) x y y = f ( x ) o ( ) ( ) ( ) 0 0 0 f x + f x x − x 以直代曲 0 x ( ) 1 p x 在微分应用中已知近似公式 : 需要解决的问题 x x 的一次多项式 机动 目录 上页 下页 返回 结束
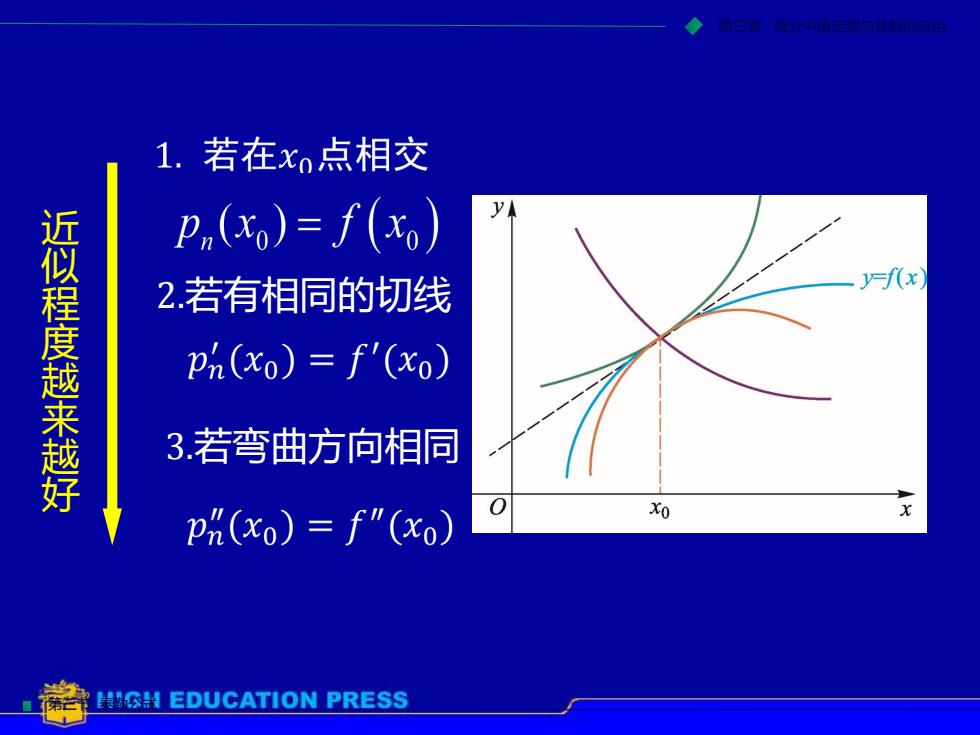
1.若在xo点相交Vp,(xo)= f (xo)近似程度越来越好y-f(x2.若有相同的切线pn(xo) = f'(xo)3.若弯曲方向相同0xoxpn(xo) = f"(xo)HH EDUCATIONPRESS
第三节 泰勒公式 第三章 微分中值定理与导数的应用 近 似 程 度 越 来 越 好 2.若有相同的切线 3.若弯曲方向相同

1.求n次近似多项式Pn(x),要求:)= f(n)(xo)Pn(xo) = f(xo), pn(xo) = f'(xo), .**, phn)(xo)Pn(x)= ao+ai(x- xo)+a2(x - xo)? + ..+ an(x - xo)n令ai+2a2(x- xo)+..+ nan(x-xo)n-1则p(x) =2 a2 +..+ n(n - )an(x - xo)n-2pn(x) =.....(n) (x)=n!anpn"中aj = pn(xo)= f(xo)ao = pn(xo)= f(xo)a2 =2P"(xo)="(xo), , an=pnn)(xo)= (n)(xo故 Pn(x)= f(xo)+ f(xo)(x-xo)+f"(xo)(x-xo)-..+ f(n)(xo)(x-xo)HIGH EDUCATION PRESS机动目录上页下页返回结束
1. 求 n 次近似多项式 要求: ( ) 2! 0 1 2 a p x n = ( ), 0 = f x , ( ) 0 ( ) ! 1 a p x n n = n n ( ) 0 ( ) f x n = 故 pn (x) = ( ) 0 f x ( )( ) 0 0 + f x x − x + 2! 1 ! 1 n n n f (x )(x x ) 0 0 ( ) + − ! 1 n 2 0 0 + f (x )(x − x ) 2! 1 机动 目录 上页 下页 返回 结束 令 pn (x) = 则 pn (x) = pn (x) = n p (n) (x) = n!a n ( ) 0 0 a p x = n ( ), 0 = f x ( ) 1 0 a p x n = ( ), 0 = f x a1 2 ( ) 2 0 + a x − x 1 0 ( ) − + + − n n n a x x 2 2 !a 2 0 ( 1) ( ) − + + − − n n n n a x x a0 n n a (x x ) a (x x ) a (x x ) 0 2 + 1 − 0 + 2 − 0 + + −

2.余项估计令R,(x)= f(x)- P,(x)(称为余项),则有R,(xo)= R′(xo) =... = R(n)(xo) = 0R,(x)(x-xo)n+1R',(EI)Rn(x)- R,(xo)(Si在xo与x之间)(x -xo)n+l- 0(n +1)(Si - xo)"R"(52)R,(E) - R'(xo)(三2 在 Xo 与与i 之间)(n+ 1)n(52 - xo)n-I(n+1)(-xo)"- 0R(n)(En) - R(n)(xo)R(n+1)(E)(在xo与x之间)(n +l)!(n+1)... 2(En - xo)- 0HIGH EDUCATION PRESS机动目录上页下页返回结束
) 0 ( 在 x 与 n 之 间 ( ) ( ) 1 0 + − = n n x x R x ( 1) 2( ) ( ) 0 ( ) n x R n n n n + − = 2. 余项估计 R (x) f (x) p (x) 令 n = − n (称为余项) , ( ) 0 R x n ( ) 0 R x n = ( ) 0 0 ( ) = = R x = n n 1 0 ( ) ( ) + − n n x x R x n n n x R ( 1)( ) ( ) 1 0 1 + − = ( 1)( ) ( ) 1 0 1 n n n x R + − = 1 2 0 2 ( 1) ( ) ( ) − + − = n n n n x R = ( 1)! ( ) ( 1) + = + n R n n 则有 ( ) 0 R x − n − 0 ( ) 0 R x n − − 0 ( ) 0 ( ) R x n − n − 0 x ) 1 0 ( 在 x 与x 之 间) 1 2 0 ( 之间 在 与 x 机动 目录 上页 下页 返回 结束