《电路》课程教学资源（PPT课件）第13章 拉普拉斯变换

4.f(t)=t" tr'fre-fd 00 -st 一St ["t"-e-"dt 当n=1 Lt川= lim e =0 t00 当n=2 21= 2 L]=川t] n. Lt"]= n+1

0 lim = → st n t e t n 4. f (t) = t L t t e dt n n −st   = 0 [ ] st n e s t −   = − 0 d n s t s t n t s e e s t d 0 0    − − = − + t e t s n n std 0 1   − − = [ ] [ ] −1 = n n L t s n L t 2 1 1 [ ] s 当n＝ L t = 3 2 2 2 [ ] s 当n＝ L t = 1 ! [ ] + = n n s n L t

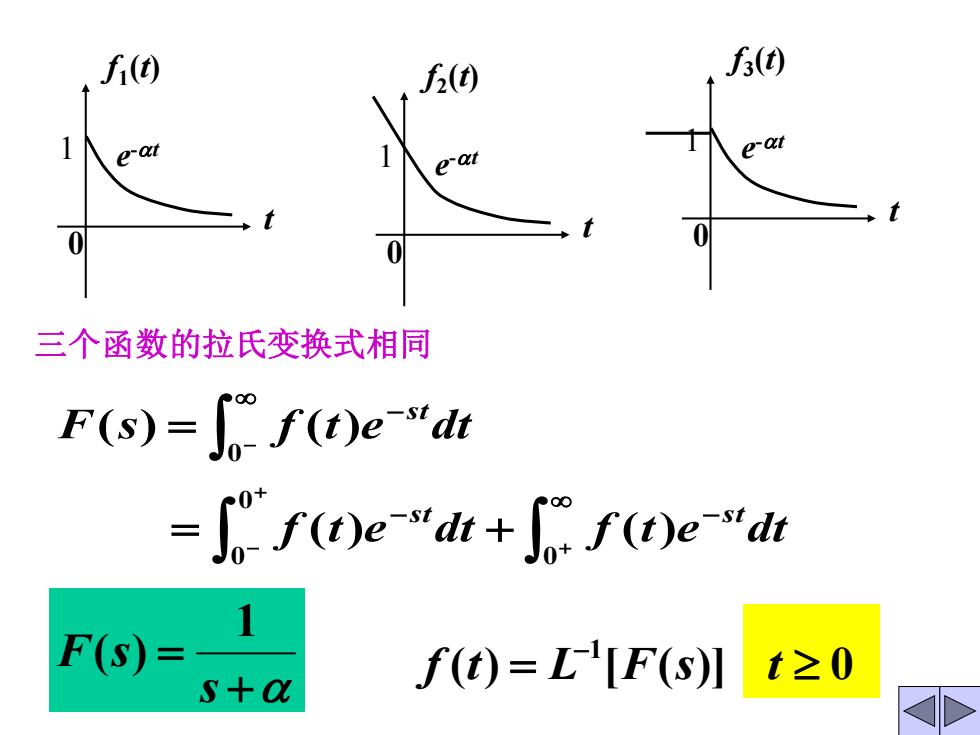
f(因 2() f3() e-at 三个函数的拉氏变换式相同 F(s)=f(t)e-"dt -"f(D)e-"dt+f(e-"dr F(S)= f(t)=L[F(s)1t≥0 s+a

1 f1 (t) e -t t 0 1 f2 (t) e -t t 0 三个函数的拉氏变换式相同 + = s F s 1 ( ) ( ) [ ( )] 0 1 =  − f t L F s t 1 f3 (t) e -t t 0 f t e dt f t e dt F s f t e dt s t s t s t     − −  − + + − − = + = 0 0 0 0 ( ) ( ) ( ) ( )

§2.拉普拉斯变换的基本性质 一.线性性质 若LLf(t]=F(S),LLf(t)】=F(s) 则af(t)±bf(t川=aF(S)士bF(s) 例：IAl= S 耳a-g1=或gd} 3:4sima网=427(e-e1

§ 2.拉普拉斯变换的基本性质 一. 线性性质 [ ( )] ( ) , [ ( )] ( ) 1 1 2 2 若L f t = F s L f t = F s 例1： L[A] 例3： L[sint] [ ( ) ( )] 1 2 则L a f t  b f t ] 1 1 [ 2 1 j S j S + j − − = ( ) ( ) 1 2 = aF s  bF s 2 2   + = S ( )] 2 1 [ j t j t e e j L  −  = − S A = 2 [ (1 )] t L A e − 例 ： − ) 1 1 ( + = − s s A

二.时域导数性质 设：LLf(t川=F(s) 41=-) :Leos1=d（(in@II o dt ) s2+0 例2：460=440=s×g80。-l

二. 时域导数性质 ] ( ) (0 ) ( ) [ − = sF s − f dt df t L [ sin ] 1 2 2 0 − − + = t s s     2 2 + = s s (sin )] 1 1 [cos ] [ t dt d L t L   例 ：  = 例2：L[ (t)] [ (t)] dt d = L  ( ) 1 1 0 =  − t − = S S  设：L[ f (t)] = F(s)

三.时域的积分性质 设：Lf(t川=F(s) f(drl=-F(s) 例L)=可旷(5)d51 L[e(t)_1 S s2

三. 时域的积分性质 ( ) 1 [ ( ) ] 0 F s s L f d t =  −   例 L[t] 2 [ ( )] 1 s s L t = =  [ ( ) ] 0 − = t L   d 设：L[ f (t)] = F(s)