
·2· 第一章概率论的基本概念 个试验可以在相同的条件下重复地进行.又如试验E6,我们知道灯泡的寿命(以 小时计)≥0,但在测试之前不能确定它的寿命有多长.这一试验也可以在相同 的条件下重复地进行,概括起来,这些试验具有以下的特点 1°可以在相同的条件下重复地进行; 2°每次试验的可能结果不止一个,并且能事先明确试验的所有可能 结果; 3°进行一次试验之前不能确定哪一个结果会出现 在概率论中,我们将具有上述三个特点的试验称为随机试验. 本书中以后提到的试验都是指随机试验。 我们是通过研究随机试验来研究随机现象的. §2样本空间、随机事件 (一)样本空间 对于随机试验,尽管在每次试验之前不能预知试验的结果,但试验的所有可 能结果组成的集合是已知的.我们将随机试验E的所有可能结果组成的集合称 为E的样本空间,记为S.样本空间的元素,即E的每个结果,称为样本点. 下面写出§1中试验E4(k=1,2,.,7)的样本空间S: S:{H,T}; S::(HHH,HHT,HTH,THH,HTT,THT,TTH,TTT); S1:{0,1,2,3}: S:{1,2,3,4,5,6}: S5:{0,1,2,3,.}; S6:{tlt≥0}; S,:{(x,y)川T≤x≤y≤T,这里x表示最低温度(℃),y表示最高温度 (℃).并设这一地区的温度不会小于T。,也不会大于T. (二)随机事件 在实际中,当进行随机试验时,人们常常关心满足某种条件的那些样本点所 组成的集合.例如,若规定某种灯泡的寿命(小时)小于500为次品,则在E。中我 们关心灯泡的寿命是否有t≥500.满足这一条件的样本点组成S。的一个子集 A={tt≥500}.我们称A为试验E6的一个随机事件.显然,当且仅当子集A中 的一个样本点出现时,有t≥500

§2样本空间、随机事件 ·3· 一般,我们称试验E的样本空间S的子集为E的随机事件,简称事件①.在 每次试验中,当且仅当这一子集中的一个样本点出现时,称这一事件发生 特别,由一个样本点组成的单点集,称为基本事件.例如,试验E,有两个基 本事件{H}和{T;试验E,有6个基本事件1),{2,{6. 样本空间S包含所有的样本点,它是S自身的子集,在每次试验中它总是 发生的,S称为必然事件.空集必不包含任何样本点,它也作为样本空间的子集, 它在每次试验中都不发生,必称为不可能事件。 下面举几个事件的例子 例1在E,中事件A:“第一次出现的是H”,即 A,=(HHH,HHT,HTH,HTT). 事件A2:“三次出现同一面”,即 A:=(HHH,TTT). 在E6中,事件A:“寿命小于1000小时”,即 Ag={t0≤t<1000}. 在E,中,事件A:“最高温度与最低温度相差10摄氏度”,即 A,={(x,y)ly-x=10,T≤x≤y≤T. ◇ (三)事件间的关系与事件的运算 事件是一个集合,因而事件间的关系与事件的运算自然按照集合论中集合 之间的关系和集合运算来处理.下面给出这些关系和运算在概率论中的提法.并 根据“事件发生”的含义,给出它们在概率论中的含义. 设试验E的样本空间为S,而A,B,A(k=1,2,.)是S的子集。 1°若ACB,则称事件B包含事件A,这指的是事件A发生必导致事件B 发生 若ACB且BCA,即A=B,则称事件A与事件B相等. 2°事件AUB={xx∈A或x∈B}称为事件A与事件B的和事件.当且仅 当A,B中至少有一个发生时,事件AUB发生. 类似地,称UA。为n个事件A1,A2,A,的和事件;称UA.为可列 个事件A1,A2,.的和事件. 3°事件A∩B={x|x∈A且x∈B}称为事件A与事件B的积事件.当且仅 ①严格地说,事件是指S中的满足某些条件的子集。当S是由有限个元素或由可列无限个元素组 成时,每个子集都可作为一个事件。着S是由不可列无限个元素组成时,某子集必须排除在外 幸而 这种不可容许的子集在实际应用中儿平不会逼到,今后:每当我们讲列一个事件时都是假定它是容许考 虑的那种子集,读者如有兴趣可参考较详细的教材
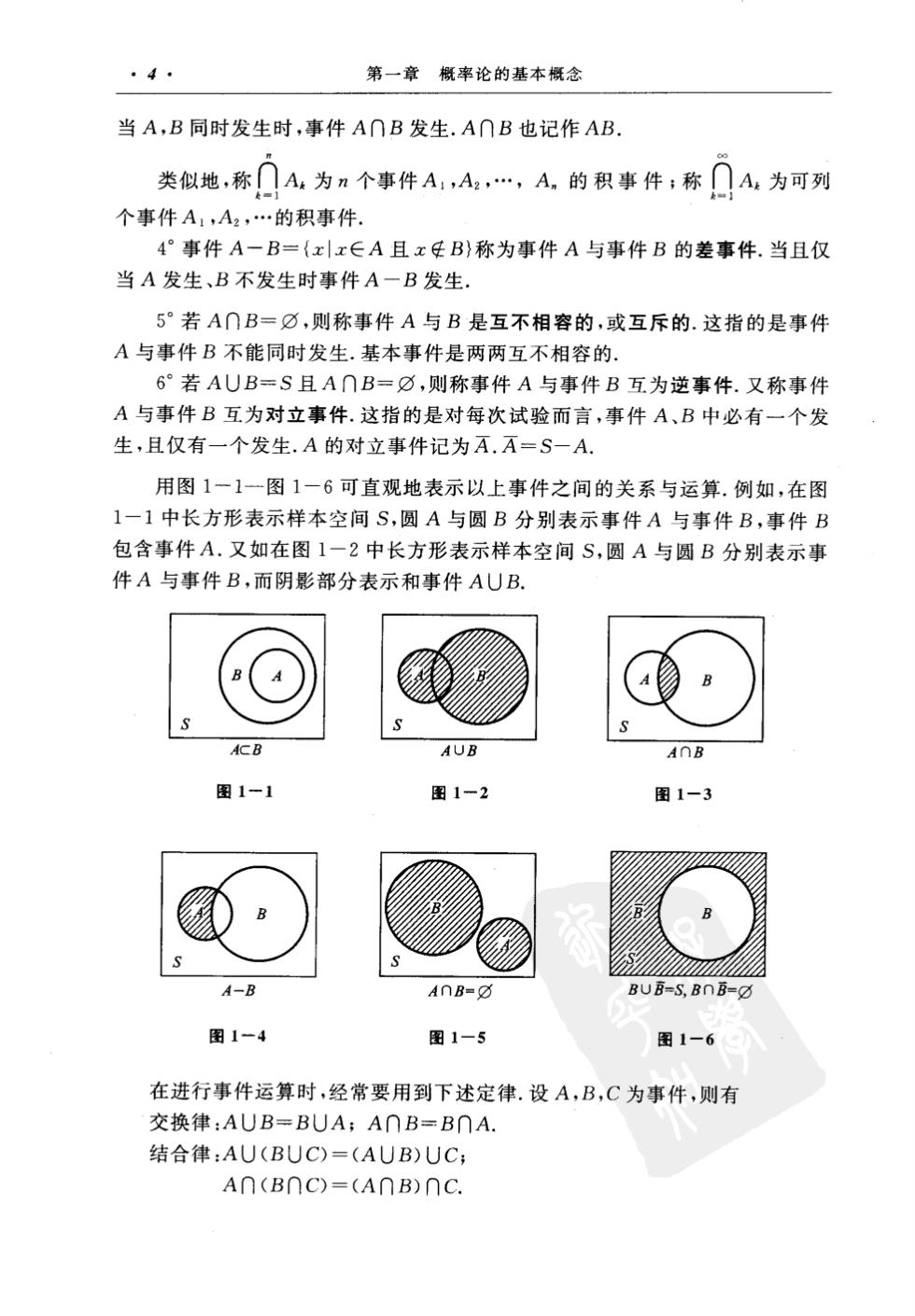
·4 第一章概率论的基本概念 当A,B同时发生时,事件A∩B发生,A∩B也记作AB 类似地,称∩A:为n个事件A,A2,A,的积事件:称∩A为可列 个事件A1,A2,.的积事件 4°事件A一B={x|x∈A且x¢B)称为事件A与事件B的差事件.当且仅 当A发生、B不发生时事件A一B发生 5°若A∩B=⑦,则称事件A与B是互不相容的,或互斥的.这指的是事件 A与事件B不能同时发生.基本事件是两两互不相容的. 6°若AUB=S且A∩B=,则称事件A与事件B互为逆事件.又称事件 A与事件B互为对立事件.这指的是对每次试验而言,事件A、B中必有一个发 生,且仅有一个发生.A的对立事件记为A.A=S-A. 用图1一1一图1一6可直观地表示以上事件之间的关系与运算.例如,在图 1一1中长方形表示样本空间S,圆A与圆B分别表示事件A与事件B,事件B 包含事件A.又如在图1一2中长方形表示样本空间S,圆A与圆B分别表示事 件A与事件B,而阴影部分表示和事件AUB. ACB AUB 图1-1 图1-2 图1-3 )B AnB= BUB=S,BnB= 图1-4 图1-5 图1-6 在进行事件运算时,经常要用到下述定律.设A,B,C为事件,则有 交换律:AUB=BUA;A∩B=B∩A. 结合律:AU(BUC)=(AUB)UC; An(B∩C)=(A∩B)∩C

§3频率与概率 5 分配律:AU(B∩C)=(AUB)∩(AUC): A∩(BUC)=(A∩B)U(A∩C). 德摩根律:AUB=A∩B;A∩B=AUB 例2在例1中有 A UA:=(HHH,HHT,HTH,HTT,TTT), A,∩A2={HHH}, A:-A=(TTT), A UA=(THT,TTH,THH). 例3如图1一7所示的电路中,以A表示“信 号灯亮”这一事件,以B,C,D分别表示事件:继电器 接点I,I,I闭合,那么容易知道BCCA,BDCA, BCUBD=A,而BA=⑦,即事件B与事件A互不 相容.又,BUC=B∩C.(左边表示事件“I,Ⅱ至少 有一个闭合”的逆事件,也就是I,Ⅱ都不闭合, 图1-7 B,C同时发生·) ◇ §3频率与概率 对于一个事件(除必然事件和不可能事件外)来说,它在一次试验中可能发 生,也可能不发生.我们常常希望知道某些事件在一次试验中发生的可能性究竞 有多大.例如,为了确定水坝的高度,就要知道河流在造水坝地段每年最大洪水 达到某一高度这一事件发生的可能性大小.我们希望找到一个合适的数来表征 事件在一次试验中发生的可能性大小.为此,首先引入频率,它描述了事件发生 的频繁程度,进而引出表征事件在一次试验中发生的可能性大小的数一概率。 (一)频率 定义在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的 次数称为事件A发生的频数.比值A/n称为事件A发生的频率,并记成 f(A). 由定义,易见频率具有下述基本性质: 1°0≤f.(A)≤1: 2°f.(S)=1: 3°若A,A2,A是两两互不相容的事件,则 f,(AUA2U.UA)=fn(A1)+f,(Az)+.+f(A). 由于事件A发生的频率是它发生的次数与试验次数之比,其大小表示A发
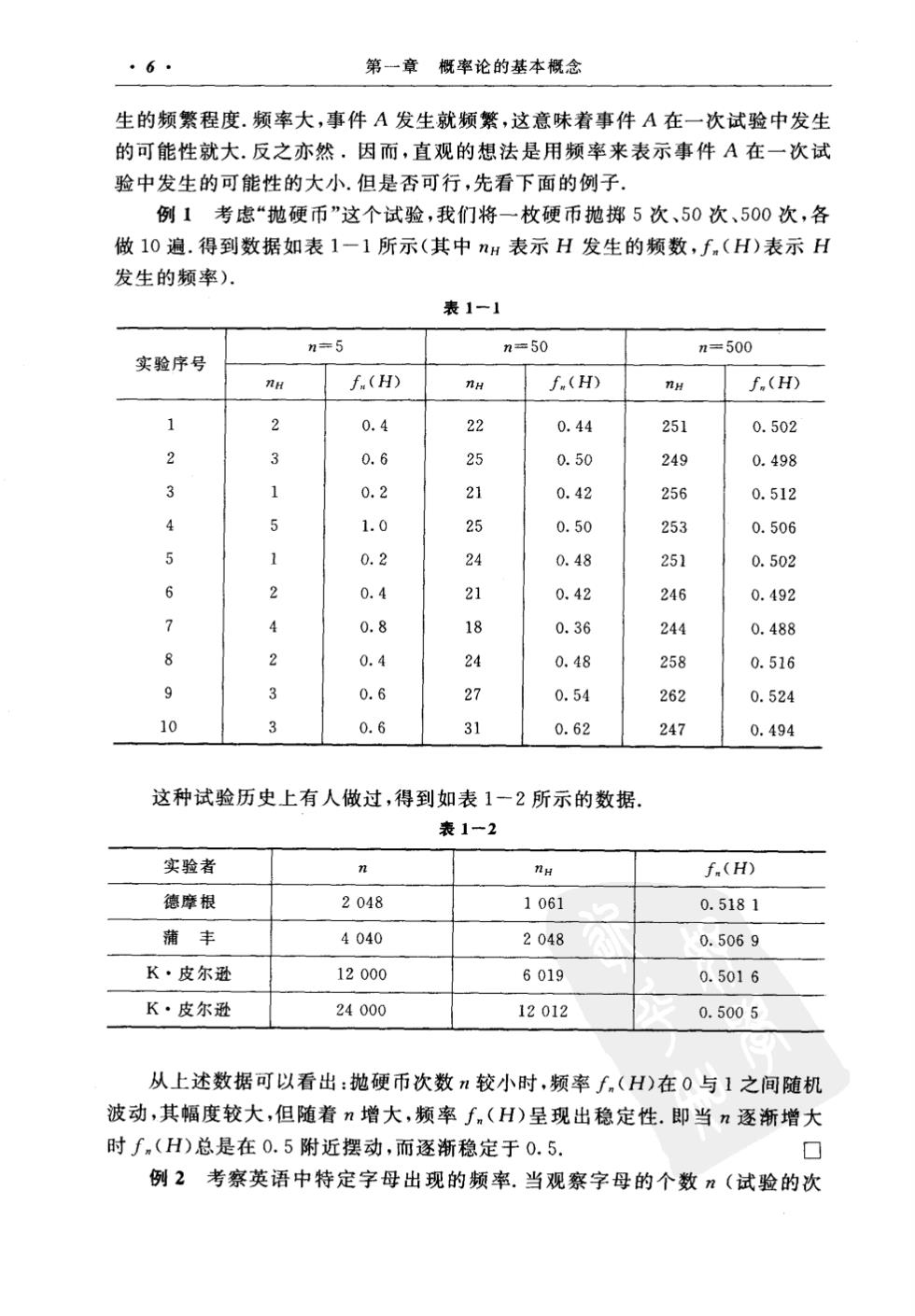
6 第一章概率论的基本概念 生的频繁程度.频率大,事件A发生就频繁,这意味着事件A在一次试验中发生 的可能性就大.反之亦然,因而,直观的想法是用频率来表示事件A在一次试 验中发生的可能性的大小.但是否可行,先看下面的例子 例1考虑“抛硬币”这个试验,我们将一枚硬币抛掷5次、50次、500次,各 做10遍.得到数据如表1一1所示(其中nH表示H发生的频数,f,(H)表示H 发生的频率) 表1-1 n=5 n=50 n✉500 实验序号 ∫.(H) f.(H) f.(H) 1 2 0.4 22 0.44 251 0.502 2 3 0.6 25 0.50 249 0.498 3 1 0.2 21 0.42 256 0.512 5 1.0 25 0.50 253 0.506 0.2 0.48 251 0.502 6 0.4 21 0.42 246 0.492 2 0.8 18 0.36 244 0.488 0.4 24 0.48 258 0.516 9 0.6 3 0.54 262 0.524 10 3 0.6 9 0.62 247 0.494 这种试验历史上有人做过,得到如表1一2所示的数据. 表1一2 实验者 f.(H) 德摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 K·皮尔逊 12000 6019 0.5016 K·皮尔逊 24000 12012 0.5005 从上述数据可以看出:抛硬币次数n较小时,频率∫(H)在0与1之间随机 波动,其幅度较大,但随着n增大,频率f.(H)呈现出稳定性.即当n逐渐增大 时∫.(H)总是在0.5附近摆动,而逐渐稳定于0.5. 例2考察英语中特定字母出现的频率.当观察字母的个数”(试验的次