
HHHHHHHHHHHHHHHHHHHHHHlal-a+a,+a向量模的坐标表示式向量方向余弦的坐标表示式acoSα =+a+aacos β =ax+a,+a,acOs Y=(cos α + cos° β+ cos°= 1)ax+a,+a,上页反回下页
2 2 2 | | a = ax + ay + az 向量模的坐标表示式 2 2 2 cos x y z x a a a a + + = 2 2 2 cos x y z y a a a a + + = 2 2 2 cos x y z z a a a a + + = 向量方向余弦的坐标表示式 ( cos cos cos 1 ) 2 2 2 + + =

HHHHHHHHHHHHHHHHHHHHHHH(点积、内积)4、数量积a.b-lallblcose其中θ为a与b 的夹角数量积的坐标表达式a.b=ab+a,b,+a,b两向量夹角余弦的坐标表示式a.b+a.b.+a.bcosA =a*+a, +a?b,+b,+balba,b+a,b,+a,b, =0上页这回下页
4、数量积 a b | a || b | cos = 其中 为a 与b 的夹角 (点积、内积) a b = axbx + ayby + azbz 数量积的坐标表达式 a b ⊥ axbx + ayby + azbz = 0 2 2 2 2 2 2 cos x y z x y z x x y y z z a a a b b b a b a b a b + + + + + + = 两向量夹角余弦的坐标表示式

HHHHHHHHHHHHHHHHHHHHHHH5、向量积(叉积、外积)c -| a l b ] sin其中θ为a与b 的夹角c的方向既垂直于a,又垂直b,指向符合右手系向量积的坐标表达式axb =(a,b,-a,b,)i +(ab,-a,b,)j+(a,b, -a,br)k页下页回
5、向量积 | c | | a || b |sin = 其中 为a 与b 的夹角 c 的方向既垂直于a ,又垂直于b ,指向符合 右手系. (叉积、外积) a b a b k a b a b i a b a b j x y y x y z z y z x x z ( ) ( ) ( ) + − = − + − 向量积的坐标表达式 a b

HHHHHHHHHHHHHHHHHHHHHHHiikaxb=axa, azbb,b.aaallbbb,b6、混合积axaya2[abc] =(axb).c=bb,b,cxCzc、上页下页友回
x y z x y z b b b a a a i j k a b = a b // z z y y x x b a b a b a = = [abc] a b c = ( ) x y z x y z x y z c c c b b b a a a = 6、混合积
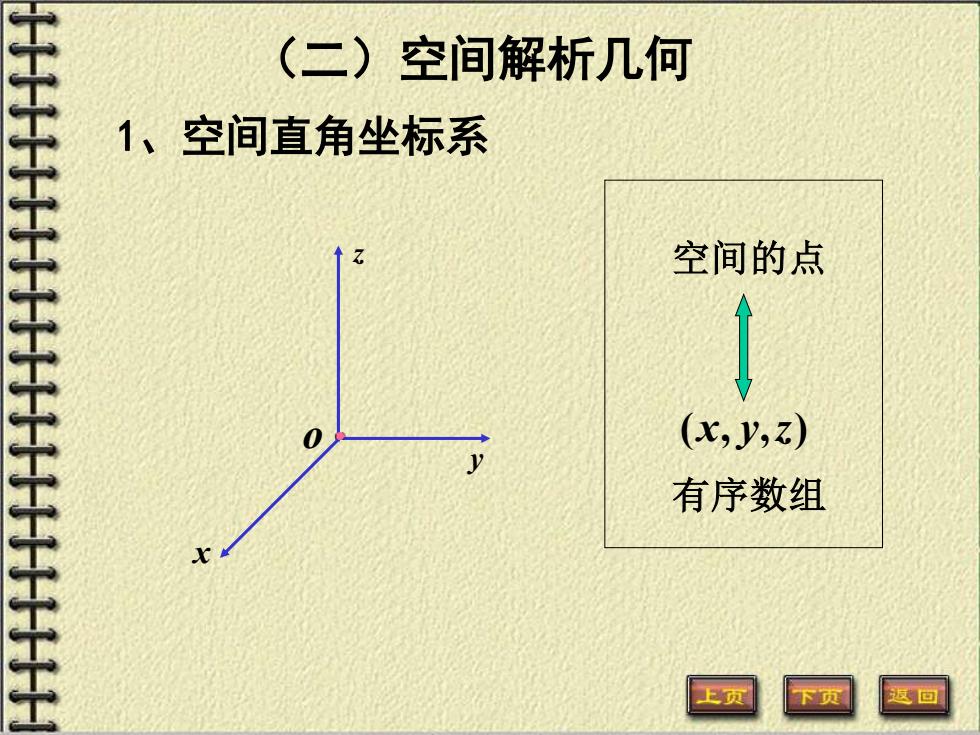
HHHHHHHHHHHHHHHHHHHHHH(一)空间解析几何1、空间直角坐标系空间的点(x,y,z)0有序数组?页回下页
x y z o 1、空间直角坐标系 空间的点 有序数组 (x, y,z) (二)空间解析几何