
导航 准线方程 号 号 号 范围 x≥0y∈R s0y∈R x∈Ry20 x∈RJyS0 对称轴 x轴 x轴 y轴 y轴 顶点 (0,0) 离心率 e=1
导航 准线方程 x=- 𝐩 𝟐 x= 𝐩 𝟐 y=- 𝐩 𝟐 y= 𝐩 𝟐 范围 x≥0,y∈R x≤0,y∈R x∈R,y≥0 x∈R,y≤0 对称轴 x 轴 x 轴 y 轴 y 轴 顶点 (0,0) 离心率 e=1
导航 3.做一做:抛物线x2=y的焦点坐标为 ;准线方程 为 ;顶点坐标为 ;对称轴为 离心率为 答案:(0,)=(0,0)y轴1
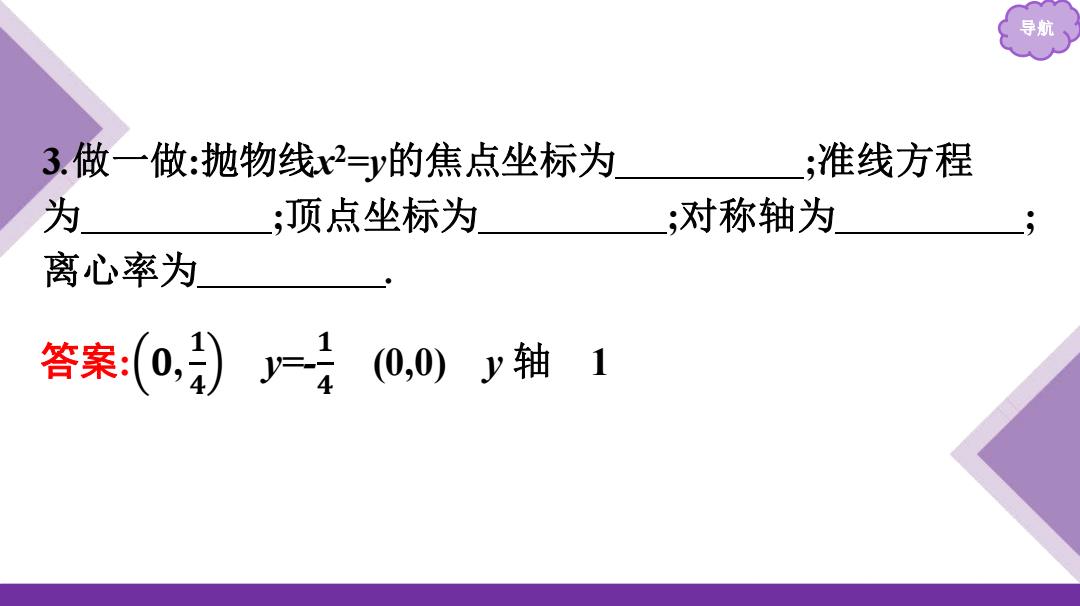
导航 3.做一做:抛物线x 2=y的焦点坐标为 ;准线方程 为 ;顶点坐标为 ;对称轴为 ; 离心率为 . 答案: 𝟎, 𝟏 𝟒 y=- 𝟏 𝟒 (0,0) y 轴 1

导航 【思考辨析】 判断正误(正确的画“V,错误的画“X”) (1)方程x2=2py中的x的取值范围为[0,+oo).( (2)抛物线x2=-2py(p>0)的对称轴为y轴.() (3)已知直线AB过抛物线y2=2x(p>0)的焦点,与该抛物线交于 点A,B.若Ax1,Bx22),则ABx1t比2+.()
导航 【思考辨析】 判断正误.(正确的画“√”,错误的画“×”) (1)方程x 2=2py中的x的取值范围为[0,+∞).( × ) (2)抛物线x 2=-2py(p>0)的对称轴为y轴.( √ ) (3)已知直线AB过抛物线y 2=2px(p>0)的焦点,与该抛物线交于 点A,B.若A(x1 ,y1 ),B(x2 ,y2 ),则|AB|=x1+x2+ .( × ) 𝒑 𝟐

导航 课堂·重难突破 探究一根据抛物线的几何性质求其标准方程 【例1】抛物线的顶点在原点,对称轴与椭圆x2+4y2=36的短 轴所在的直线重合,抛物线的焦点到顶点的距离为3,求抛物线 的方程 分析:先确定抛物线的焦点位置,再求其方程
导航 课堂·重难突破 探究一 根据抛物线的几何性质求其标准方程 【例1】抛物线的顶点在原点,对称轴与椭圆9x 2+4y 2=36的短 轴所在的直线重合,抛物线的焦点到顶点的距离为3,求抛物线 的方程. 分析:先确定抛物线的焦点位置,再求其方程

导航 解:根据题意,可知抛物线的对称轴为x轴,设抛物线的方程为 y2=x(a≠0). 又抛物线的焦点到顶点的距离为3,则有=3,故=士12. 故抛物线的方程为y2=12x或y2=-12x
导航 解:根据题意,可知抛物线的对称轴为x轴,设抛物线的方程为 y 2=ax(a≠0). 又抛物线的焦点到顶点的距离为3,则有 =3,故a=±12. 故抛物线的方程为y 2=12x或y 2=-12x. 𝒂 𝟒