
三.反函数 一对一的函数 定义:设y=f(x),x∈X,y∈Y如果对于Y内的任一y, X内都有唯一确定的x与之对应,则在Y上确定了一个 函数,称为y=f(x)的反函数,记作x=f(y) 习惯上,x作为自变量,反函数记作y=(x) 例1求y=3x-1的反函数 解:由y=3x-1,得x=牛,互换和,反函数为=x+1 3 3
三. 反函数 1 1 ( ), X . , Y ( ) ( ). ( ). y f x x y Y Y y X x y f x x f y x y f x − − = = = = 定义:设 , 如果对于 内的任一 内都有唯一确定的 与之对应,则在 上确定了一个 函数,称为 的反函数,记作 习惯上, 作为自变量,反函数记作 1 1 3 1 . 3 3 y x y x x x y y + + 解:由 = − = = ,得 ,互换 和 ,反函数为 例1 求y = 3x−1的反函数. 一对一的函数
三.反函数 1.函数的定义域和值域分别是反函数的值域和定义域 2.函数与它的反函数的图像关于直线y=x对称. y=f(x) y=x Q(b,a) y=f(x) 0】 P(a,b) 3.单调函数存在反函数,且具有相同单调性
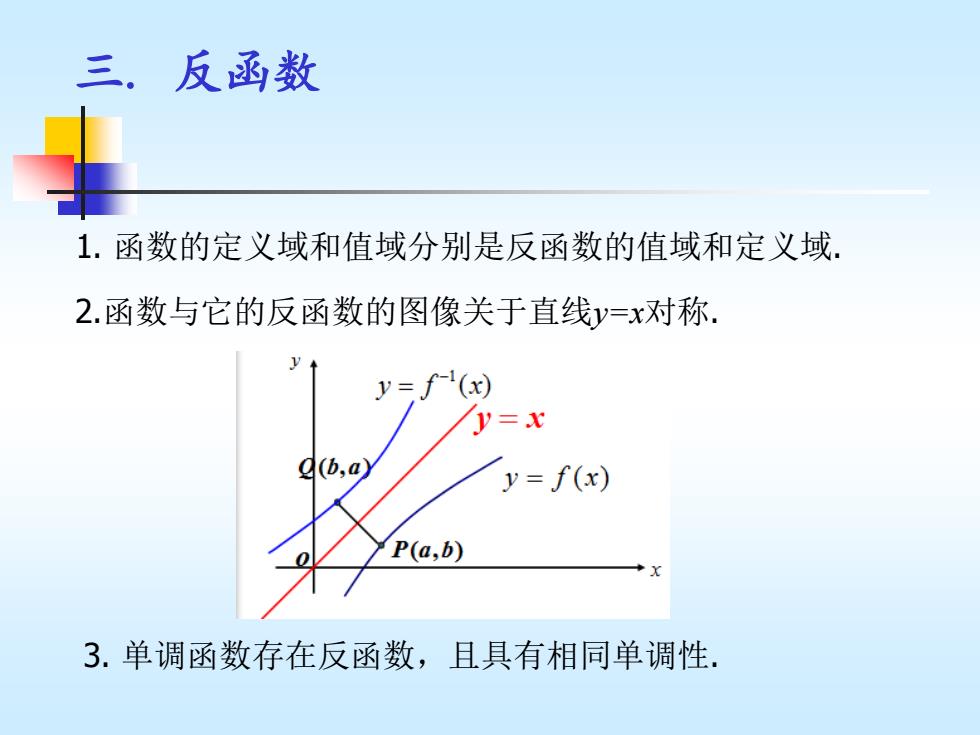
三. 反函数 3. 单调函数存在反函数,且具有相同单调性. 1. 函数的定义域和值域分别是反函数的值域和定义域. 2.函数与它的反函数的图像关于直线y=x对称