
数学模型方法 Mathematical Modeling Method
数学模型方法 Mathematical Modeling Method
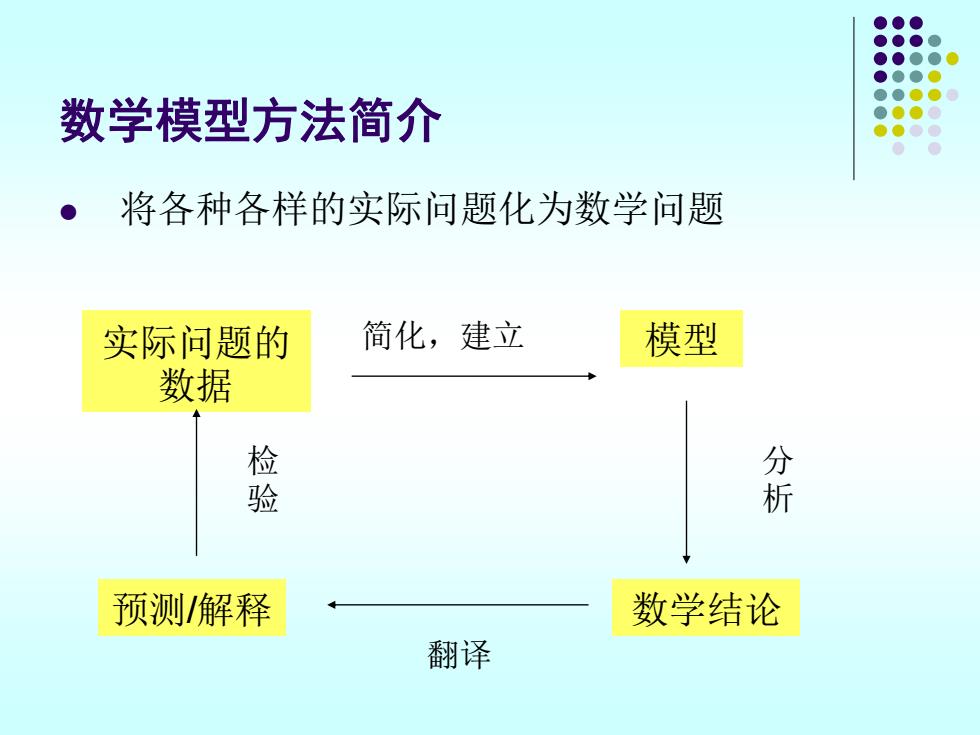
数学模型方法简介 ·将各种各样的实际问题化为数学问题 实际问题的 简化,建立 模型 数据 检 分 预测/解释 数学结论 翻译
数学模型方法简介 ⚫ 将各种各样的实际问题化为数学问题 实际问题的 数据 模型 预测/解释 数学结论 简化,建立 翻译 分 析 检 验

数学模型方法简介 构建数学模型的步骤和方法 (1)识别问题,确定变量与常量; (2)采用数学符号,建立自变量和应变量以及常 量之间的关系一数学模型; (3)在模型上进行必要的逻辑推理和演算,求得 模型的解答 (4)返回到实际问题中进行检验!
构建数学模型的步骤和方法 数学模型方法简介 (1) 识别问题,确定变量与常量; (2) 采用数学符号,建立自变量和应变量以及常 量之间的关系——数学模型; (3) 在模型上进行必要的逻辑推理和演算,求得 模型的解答 (4) 返回到实际问题中进行检验

数学模型方法举例 。例1.单利与复利模型 单利:设P是本金,为计息期的利率,n是计息 期数,I是n个计息期应付的单利,p为本利和. 单利模型: p=Po+l=Po+Porn=po(1+rn)
数学模型方法举例 ⚫ 例1. 单利与复利模型 单利: 设 是本金,r为计息期的利率,n是计息 期数,I是n个计息期应付的单利,p为本利和. 单利模型: 0 p p p I p p rn p rn = = + = + 0 0 0 0 + (1 )

数学模型方法举例 。例1.单利与复利模型 复利:设Po是本金,为单位计息期的利率,是 计息期数,如果每期结算一次,即前一期结束 的本利和作为下一期的本金,p为本利和. 复利模型: P=Po+Por=Po(1+r) P2=P+Pr=P(1+r)+P(1+r)r=p(1+r)2 P,=p(1+r)
数学模型方法举例 ⚫ 例1. 单利与复利模型 复利:设 是本金,r为单位计息期的利率,t是 计息期数,如果每期结算一次,即前一期结束 的本利和作为下一期的本金,p为本利和. 0 p 1 0 0 0 2 2 1 1 0 0 0 0 (1 ) (1 ) (1 ) (1 ) . (1 )t t p p p r p r p p p r p r p r r p r p p r = + = + = + = + + + = + = + 复利模型: