
第四章导数的应用问题一洛比达法则、函数的性质与图像 教学要求(①)了解三个中值定理的条件和结论,能做出几何解释(1课时): ②)掌握应用洛必达法则求型,。型不定式极限的方法(2课时: (3)掌握判断函数单调性的法则,理解并会利用导数判断函数的单 调性,理解并会利用导数计算函数的极值(2课时) 教学重点应用洛必达法则求极限:利用导数判断函数的单调性及求极值 教学难点中值定理:0°,1,∞°型未定式极限的计算:判断函数的单调性 第一节连接局部与整体的纽带 一中值定理 中值定理揭示了函数在某区间的整体性质与该区间内部某一点的导数之间的关 系,因而称为中值定理。中值定 里既是用微分学解决实际问题的理论基础,又是解 决微分学自身发展的一种理论性数学模型,因而也称为微分基本定理 一、费马定理 1.函数极值: 设函数y=(x)在点x的某领域有定义,如果对于该领域内任何异于x的x值,都 有fx)≤fx)(或x)≥fx),则称函数y=fx)在点x处取得极大值(或极小值) :),而x。成为函数f(x)的极大点(或极小点). y=f(x) 说明:函数极值是个局部性概念,极大值不一定大于极小值。 2.费马定理(可导函数取得极值的必要条件):若点x。是函数f(x)的极值点, 且fx)在处可导,则有f(x)=0 证明从略.导数为零的点成为驻点或稳定点。 说明:(1)驻点(稳定点)与极值点的关系:可导函数的极值点一定是驻点.反过 来,驻点未必是极值点。例如,fx)=x在x=0处. (2)函数的不可导点也可能是极值点。例如,yx在点x0处 二、拉格朗日中值定理 定理1(拉格朗日):如果函数fx)满足(1)在闭区间[a,b1上连续:(2)在开
1 第四章 导数的应用问题-洛比达法则、函数的性质与图像 教学要求 (1)了解三个中值定理的条件和结论,能做出几何解释(1 课时); (2)掌握应用洛必达法则求 0 0 型,0 0 型不定式极限的方法(2 课时); (3)掌握判断函数单调性的法则,理解并会利用导数判断函数的单 调性,理解并会利用导数计算函数的极值(2 课时). 教学重点 应用洛必达法则求极限;利用导数判断函数的单调性及求极值 教学难点 中值定理; 0 0 0 1 ∞ ,∞ , 型未定式极限的计算;判断函数的单调性 第一节 连接局部与整体的纽带——中值定理 中值定理揭示了函数在某区间的整体性质与该区间内部某一点的导数之间的关 系,因而称为中值定理。中值定理既是用微分学解决实际问题的理论基础,又是解 决微分学自身发展的一种理论性数学模型,因而也称为微分基本定理。 一、费马定理 1. 函数极值: 设函数 y f = ( ) x 在点 0 x 的某领域有定义,如果对于该领域内任何异于 0 x 的 x 值,都 有 0 0 f ( ) ( ) ( ( ) ( )) x ≤ ≥ f x 或f x f x ,则称函数 y f = ( ) x 在点 0 x 处取得极大值(或极小值) 0 f ( ) x ,而 0 x 成为函数 f ( ) x 的极大点(或极小点). 说明:函数极值是个局部性概念,极大值不一定大于极小值。 2.费马定理(可导函数取得极值的必要条件):若点 0 x 是函数 f ( ) x 的极值点, 且 f ( ) x 在 0 x 处可导,则有 0 f x'( ) 0 = . 证明从略. 导数为零的点成为驻点或稳定点. 说明:(1)驻点(稳定点)与极值点的关系:可导函数的极值点一定是驻点. 反过 来,驻点未必是极值点。例如, 3 f ( )= x x 在 x=0处. (2) 函数的不可导点也可能是极值点。例如, y =| | x 在点x=0处。 二、拉格朗日中值定理 定理1(拉格朗日):如果函数 f ( ) x 满足(1)在闭区间[,] a b 上连续;(2)在开
区间(a,b)上可导,那么在开区间(a,b)内至少存在一点5,使得 f3=fb-f@Eea.6》 此公式成为拉格朗日公式 说明:()拉格朗日公式右端表示函数在区间[a,b上整体变化的平均变化率,左端 表示内点x,处的局部变化率,因此拉格朗日定理是连结局部与整体的纽带。 ?)物理意义是整休上的平均速府等于某一内占计刻的瞬时速 (3)函数fx)在区间(a,b)内导数恒为零,则fx)在区间(a,b)内是常数 定理2(罗尔)如果函数f(x)满足(I)在闭区间[a,b]上连续:(2)在开区间(a,b) 上可导,3)f(@)=b,那么在开区间(a,b)内至少存在一点5,使得"(5)=0. 说明:罗尔定理是拉格朗日中值定理的特例(见下图)
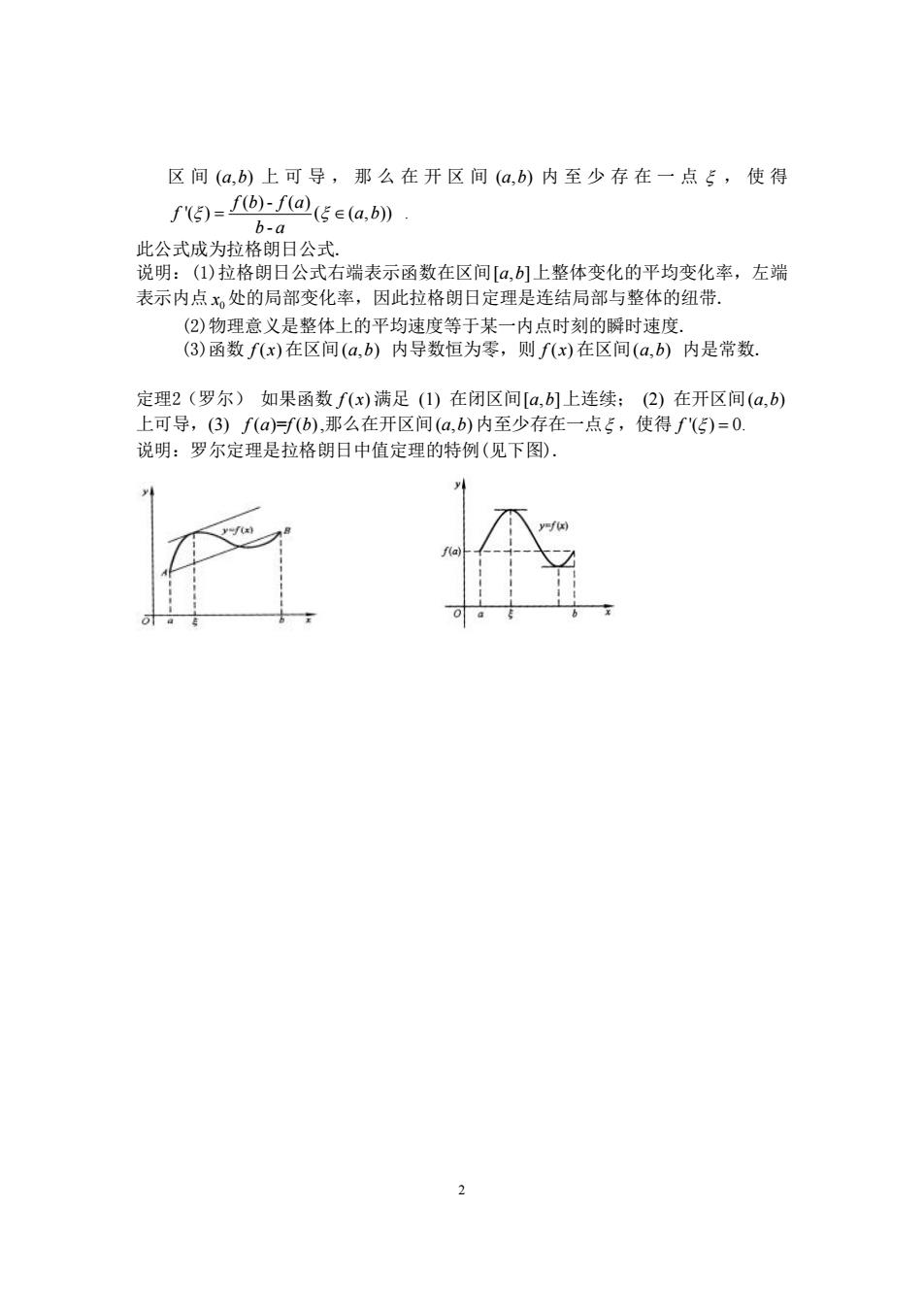
2 区 间 (,) a b 上可导,那么在开区间 (,) a b 内至少存在一点 ξ ,使得 ( )- ( ) '( ) ( ( , )) - fb fa f a b b a ξ ξ = ∈ . 此公式成为拉格朗日公式. 说明:(1)拉格朗日公式右端表示函数在区间[,] a b 上整体变化的平均变化率,左端 表示内点 0 x 处的局部变化率,因此拉格朗日定理是连结局部与整体的纽带. (2)物理意义是整体上的平均速度等于某一内点时刻的瞬时速度. (3)函数 f ( ) x 在区间(,) a b 内导数恒为零,则 f ( ) x 在区间(,) a b 内是常数. 定理2(罗尔) 如果函数 f ( ) x 满足 (1) 在闭区间[,] a b 上连续; (2) 在开区间(,) a b 上可导,(3) f ( )= ( ) a f b ,那么在开区间(,) a b 内至少存在一点ξ ,使得 f '( ) 0. ξ = 说明:罗尔定理是拉格朗日中值定理的特例(见下图)

第二节计算不定式极限的一般方法—洛必达法则 在第二章介绍极限时,对。型,。型不定式的极限都是具体问恩具体分析。本 节将用导数做工具,给出计算不定式极限的一般方法,即洛必达(L'hospital,法, 1661-1704法则 一、两个基本类型不定式 18型不定式 定理1.如果函数fx)和g(x)满足(①)1imf(x)=01img(x)=0(同一极限变化过程) ②)了和g存在,且g)≠0,③)田的极限存在(或为无穷大),则 g'(x) mf-limf因 8x) 8 说明:如果得还是,且了似也符合定理中的条件,则可维续使用洛 必达法则,即m因=1m=1im因 8( "g'(x) 2”型不定式 定理2.如果函数f(x)和g(x)满足()imf(x)=o limg(x)=w(同一极限变化过程) ②)f)和g存在,且g)≠G,(6)的极限存在(或为无穷大,则 g(x) m得m得 说明:如果代田还是”型,且了x和g也符合定理中的条件,则可继续使用洛 g(x) 多达法斯、即m得-m得m得 例1.用洛必达法则计算下列极限 ②)mx2 x-X )=g④2工 解:0数四 2- 回8数,四
3 第二节 计算不定式极限的一般方法——洛必达法则 在第二章介绍极限时,对 0 0 型, 0 0 型不定式的极限都是具体问题具体分析。本 节将用导数做工具,给出计算不定式极限的一般方法,即洛必达(L’hospital,法, 1661-1704)法则. 一、两个基本类型不定式 1. 0 0 型不定式 定理1. 如果函数 f ( ) x 和 g( ) x 满足 (1) lim ( )=0 f x lim ( )=0 g x (同一极限变化过程) (2) f x gx gx '( ) '( ) '( ) 0; 和 存在,且 ≠ (3) '( ) '( ) f x g x 的极限存在(或为无穷大),则 ( ) '( ) lim lim ( ) '( ) f x fx g x gx = . 说明:如果 '( ) '( ) f x g x 还是 0 0 型,且 f '( ) '( ) x gx 和 也符合定理中的条件,则可继续使用洛 必达法则,即 ( ) '( ) ''( ) lim lim = lim ( ) '( ) ''( ) f x fx f x g x gx g x = . . 2. ∞ ∞ 型不定式 定理2. 如果函数 f ( ) x 和 g( ) x 满足 (1) lim ( )= f x ∞ lim ( )= g x ∞ (同一极限变化过程) (2) f x gx gx '( ) '( ) '( ) 0; 和 存在,且 ≠ (3) '( ) '( ) f x g x 的极限存在(或为无穷大),则 ( ) '( ) lim lim ( ) '( ) f x fx g x gx = . 说明:如果 '( ) '( ) f x g x 还是 ∞ ∞ 型,且 f '( ) '( ) x 和g x 也符合定理中的条件,则可继续使用洛 必达法则,即 ( ) '( ) ''( ) lim lim = lim ( ) '( ) ''( ) f x f x f x g x g x g x = . 例1. 用洛必达法则计算下列极限. (1) 0 sin limx x → x (2) 3 3 1 -3 +2 lim - x x x → x x (3) + ln lim n x x → ∞ x (4) + -arctan 2 limx 1 x x π → ∞ . 解:(1) 0 0 型, 0 0 sin cos lim = lim =1. x x 1 x x → → x (2) 0 0 型, 3 2 3 2 1 1 -3 +2 3 -3 0 lim = lim = =0. x x - 3 -1 2 xx x → → xx x

8我-20 1 x- 二、其他类型的不定式 0以型,0四型,广型等,关键是将这些类型未定式化为洛必达法则可解决的日 型和型 2.求下列樱限0m⊙())+ 11 sin 解:①0x四型,改写为型。原式=m店 cos 回0型,通分化型.原式恤-把 11 (6)P型,m+y=me时-e时,而mxh1+早为0x∞型,所以 只字操子字1是 x
4 (3) ∞ ∞ 型, -1 ++ + ln 1/ 1 lim = lim = lim =0. nn n xx x x x →∞ →∞ →∞ x nx nx (4) 0 0 型, 2 2 2 + + ++ 2 -1 -arctan 1+ 2 2 lim = lim = lim = lim =1. 1 1 1+ 2 - x x xx x x x x x x x x π →∞ →∞ →∞ →∞ 二、其他类型的不定式 0× ∞ 型,∞ ∞- 型,1∞ 型等,关键是将这些类型未定式化为洛必达法则可解决的 0 0 型和 0 0 型. 例2.求下列极限. (1) 1 lim sin x x →∞ x (2) 1 1 1 lim( - ) x→ 1- ln x x (3) 1 lim(1 )x x→∞ x + 解:(1) 0× ∞ 型,改写为 0 0 型. 1 11 sin cos ( )' 1 = lim = lim = lim cos =1. 1/ (1/ ) ' xx x x xx →∞ →∞ →∞ xx x i 原式 (2) ∞ ∞- 型,通分化 0 0 型. 11 1 1 +1 ln -1+ 1 = lim = lim = lim = . (1- )ln 1- ln - 1 -ln + -1 xx x xx x x x x x xx x x →→ → + 原式 ∞ (3) 1∞ 型, 1 1 1 ln(1 ) lim ln(1 ) lim(1 ) = lim = x x x x x x x x e e x →∞ + + →∞ →∞ + , 而 1 lim ln(1 ) x x →∞ x + 为 0× ∞ 型,所以 2 2 1 1 (- ) 1 1 ln(1 ) 1 1 1 lim ln(1 ) lim lim 1. lim ln(1 ) = . 1 1 - x x xx x x x x x e x x x x →∞ →∞ →∞ →∞ ⋅ + + + = = =∴ +

第三节用导数研究函数的性质——单调性、极值和最值 一、函数的单调性 定理:设函数fx)在区间(a,b)内可导,则该函数在区间(a,b)内单调增加(单调减 少)的充要条件是:fx)≥0fx)s0),x∈(a,b),而fx)0只在个别点成立. 说明:1.证明由中值定理f(x2)-f(x)=∫"(5(x2-x)(x<5<x2)可得. 般的,我们用驻点(f(x)=0)将区间分成几个子区间,在这些子区间上 判定函数的单调性。 推论(函数单调性的充分条件):若f(x)在区间(a,b)内导数为正(或为负),即 f(x)>0(或f(x<0),则函数在区间(a,b)内单调增加(或单调减少). 例1求函数f(x)=(x-1).4的单调区间. 解:由f(x)=2(x-1)=0可得驻点为x=1.当x<1时,∫x)>0,当x>时,f(x)<0.所 以,函数的单调减少区间是(←,),单调增加区间是1,+). 二、函数的极值 定理(必要条件)设x)在点处具有导数,且在x,处取得极值,那末必定 f(x)=0. 注:可导函数(x)的极值点必定是它的驻点,但驻点却不一定是极值点
5 第三节 用导数研究函数的性质——单调性、极值和最值 一、函数的单调性 定理:设函数 f ( ) x 在区间(,) a b 内可导,则该函数在区间(,) a b 内单调增加(单调减 少)的充要条件是: fx fx '( ) 0( '( ) 0) ≥ ≤ , x∈(,) a b ,而 f x'( )=0只在个别点成立. 说明:1. 证明由中值定理 2 1 21 1 2 f ( ) ( ) ( )( ) ( ) x fx f x x x x − = − << ′ ξ ξ 可得. 2. 一般的,我们用驻点( '( )=0 f x )将区间分成几个子区间,在这些子区间上 判定函数的单调性。 推论(函数单调性的充分条件):若 f ( ) x 在区间(,) a b 内导数为正(或为负),即 fx fx '( )>0( '( )<0) 或 ,则函数在区间(,) a b 内单调增加(或单调减少). 例1 求函数 2 fx x ( ) ( -1) - 4 = 的单调区间. 解:由 fx x '( ) 2( -1) 0 = = 可得驻点为x=1. 当 时, 当 时, x fx x fx <1 '( ) 0; 1 '( ) 0. >> < 所 以,函数的单调减少区间是(- ,1) ∞ ,单调增加区间是(1 + ) , . ∞ 二、函数的极值 定理(必要条件)设 f ( ) x 在点 0 x 处具有导数,且在 0 x 处取得极值,那末必定 0 f x'( ) 0 = . 注:可导函数 的极值点必定是它的驻点 但驻点却不一定是极值点 f x() ,