
第2章微积分的直接基础, 函数 §2.1数列极限与函数极限 §2.2极限的性质与运算 §2.3连续函数
第2章微积分的直接基础—— 函数 §2.1 数列极限与函数极限 §2.2 极限的性质与运算 §2.3 连续函数

§2.2极限的性质与运算 1.函数极限的性质 下面仅对x→x的变化过程讨论函数极限的性质, 对x→o的情形有类似结论 定理1若imf(x)=A,且A>0(或A<0),则存 x→x 在点x,某邻域U(x,6),对一切x∈U(x,6), 恒有f(x)>0(或f(x)<0). 由于在x∈U°(x,δ), A+8 恒有f(x)>0(或f(x)<0), 称该定理为局部保号性定理 0-6 0+6
§2.2 极限的性质与运算 1.函数极限的性质 0 . x x x → → 下面仅对 的变化过程讨论函数极限的性质, 对 的情形有类似结论 0 0 ( , ), ( ) 0( ( ) 0), . x U x f x f x 由于在 恒有 或 称该定理为局部保号性定理 0 0 0 0 0 0 lim ( ) , 0( 0), ( , ), ( , ) ( ) 0( ( ) 0). x x f x A A A x U x x U x f x f x → = 若 且 或 则存 在点 某邻域 对一 定理1 切 , 恒有 或

§2.2极限的性质与运算 1.函数极限的性质 定理2若f(x)≥0,且Iimf(x)=A,那么A≥0. →X0 要注意的是,若f(x)>0,limf(x)=A, 那么A≥0. 比如,当x≠1时,函数f(x)=(x-1)2>0,但lim(x-1)2=0. 推论若f(x)≤g(x),且1Iimf(x)=A,Iimg(x)=B, 那么A≤B
§2.2 极限的性质与运算 0 ( ) 0 lim ( ) 0. x x f x f x A A → 定理2 若 = ,且 ,那么 0 ( ) 0 lim ( ) 0. x x f x f x A A → = 要注意的是,若 , , 那么 0 0 ( ) ( ) lim ( ) lim ( ) . x x x x f x g x f x A g x B A B → → = = 若 ,且 , , 那么 推论 2 2 1 1 ( ) ( 1) 0 lim( 1) 0. x x f x x x → 比如,当 = − − 时,函数 ,但 = 1.函数极限的性质

§2.2极限的性质与运算 2.无穷大量与无穷小量 (1)无穷大量 定义:若在某个极限变化过程(x→x,或→o)中, 函数f(x)的绝对值f(x)的极限是无穷大,记作 f(x)→o.称f(x)为无穷大量,或无穷大. 注:无穷大是变量,并不是非常大的有限数 “严-+心,函数)=在→时是无穷大量
§2.2 极限的性质与运算 0 ( ) ( ) ( ) ( ) . x x x f x f x f x f x → → → 定义:若在某个极限变化过程( 或 )中, 函数 的绝对值 的极限是无穷大,记作 .称 为无穷大量,或无穷大 1 1 lim , ( ) 2 2 x x x f x x →− = + = → − 函数 在 时是无穷大量. (1) 无穷大量 注:无穷大是变量,并不是非常大的有限数. 2.无穷大量与无穷小量 (1) 无穷大量
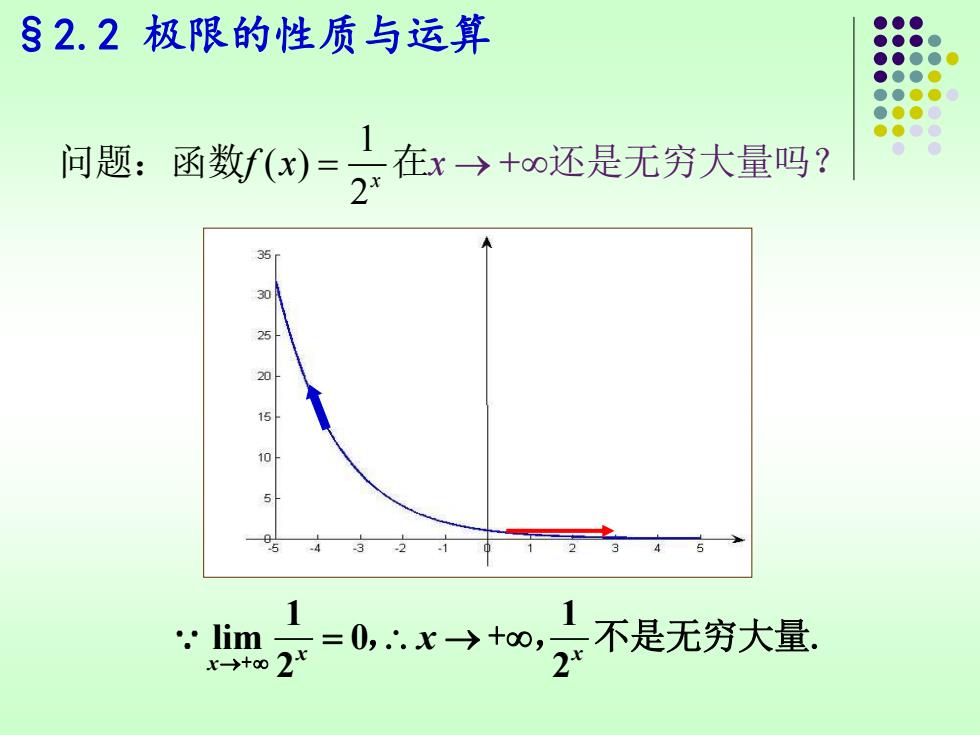
§2.2极限的性质与运算 问题:函数f(x)=在x→+∞还是无穷大量吗? 2 :m=0,x→+o,2不是无穷大量
§2.2 极限的性质与运算 1 1 lim 0 2 2 x x x x → = → + , + , 不是无穷大量. 1 ( ) 2 + x 问题:函数f x = 在x → 还是无穷大量吗?