
一, 函数的定义 举例 例3:狄利克雷函数(Dirichlet) y=D()= 当x是有理数时 0 当x是无理数时 r=a(1-sin) 例4:极坐标下的心形函数 r=a(1-sin0)
一 . 函数的定义 举例 4 r a= (1 sin ) − 例 :极坐标下的心形函数 例3:狄利克雷函数(Dirichlet) = = 当 是无理数时 当 是有理数时 x x y D x 0 1 ( )
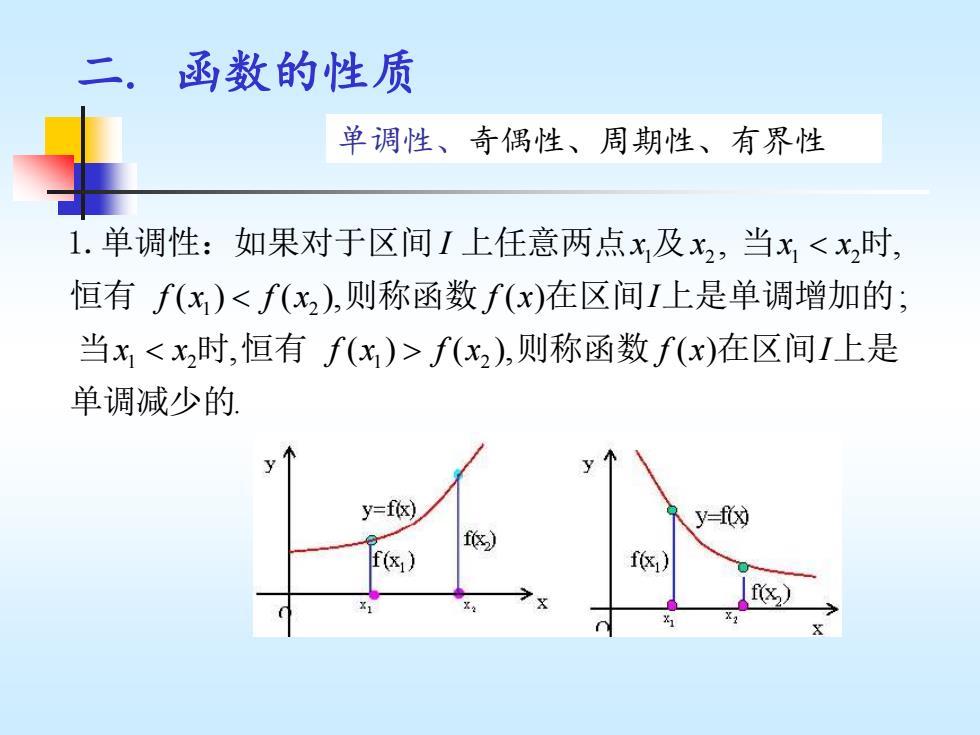
二.函数的性质 单调性、奇偶性、周期性、有界性 1.单调性:如果对于区间I上任意两点x及x2,当x<x,时, 恒有f(x)<f(x2),则称函数f(x)在区间I上是单调增加的; 当x<x2时,恒有f(x)>f(x2),则称函数f(x)在区间I上是 单调减少的 y y=fx) y-f(x) f) f(x)
二. 函数的性质 单调性、奇偶性、周期性、有界性 1 2 1 2 1 2 1 2 1 2 , , ( ) ( ), ( ) ; , ( ) ( ), ( ) . I x x x x f x f x f x I x x f x f x f x I 1.单调性:如果对于区间 上任意两点 及 当 时 恒有 则称函数 在区间 上是单调增加的 当 时 恒有 则称函数 在区间 上是 单调减少的

二。函数的性质 单调性、奇偶性、周期性、有界性 2.奇偶性:如果对于x∈D(D为对称区间),有f(-x)=f(x), 则称f(x)为偶函数,若有f(-x)=-f(x),则称f(x)为奇函数 偶函数的图像关于y轴对称,奇函数的图像关于原点对称
二. 函数的性质 ( ), ( ) ( ) ( ) ; ( ) - ( ) ( ) x D D f x f x f x f x f x f x − = − = 2.奇偶性:如果对于 为对称区间 有 , 则称 为偶函数 若有 ,则称 为奇函数. 偶函数的图像关于y轴对称,奇函数的图像关于原点对称. 单调性、奇偶性、周期性、有界性
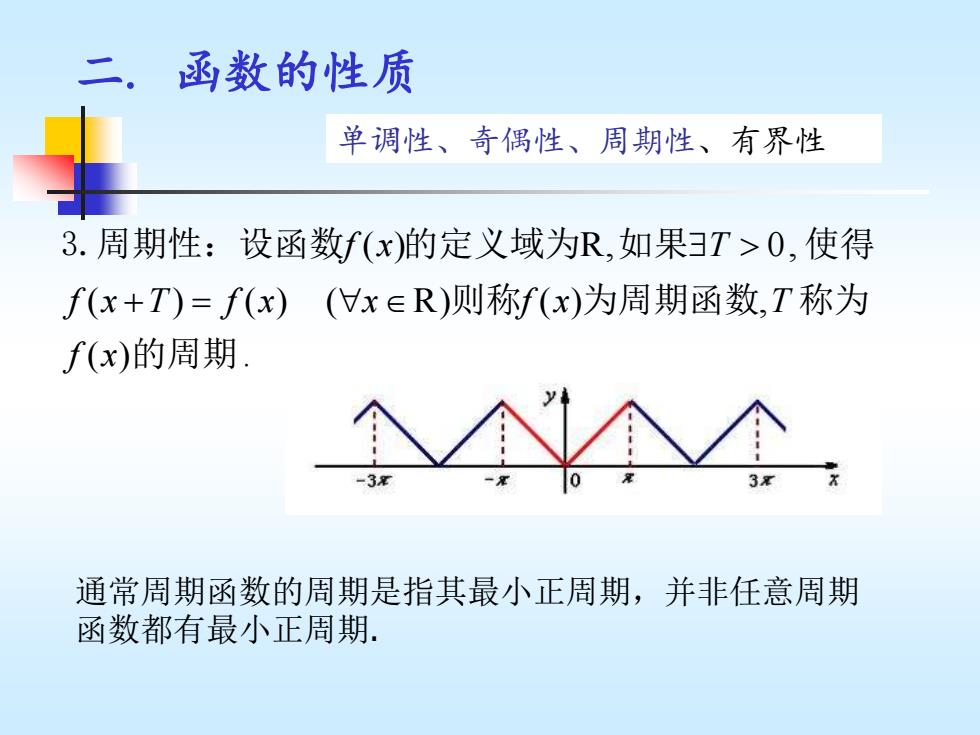
二.函数的性质 单调性、奇偶性、周期性、有界性 3.周期性:设函数f(x)的定义域为R,如果T>0,使得 f(x+T)=f(x)(x∈R)则称f(x)为周期函数,T称为 f(x)的周期. -3 3 通常周期函数的周期是指其最小正周期,并非任意周期 函数都有最小正周期
二. 函数的性质 ( ) R, 0, ( ) ( ) ( R) ( ) , ( ) . f x T f x T f x x f x T f x + = 3.周期性:设函数 的定义域为 如果 使得 则称 为周期函数 称为 的周期 通常周期函数的周期是指其最小正周期,并非任意周期 函数都有最小正周期. 单调性、奇偶性、周期性、有界性
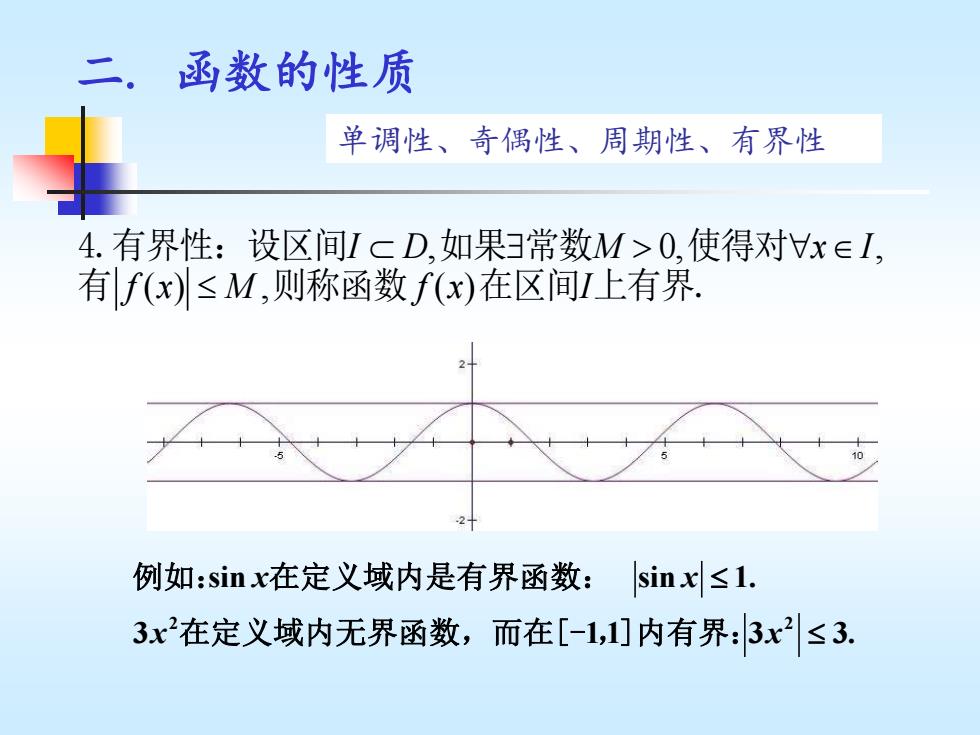
二.函数的性质 单调性、奇偶性、周期性、有界性 4.有界性:设区间IcD,如果常数M>0,使得对Vx∈I, 有f(x)≤M,则称函数f(x)在区间I上有界. 例如:sinx在定义域内是有界函数:sinx≤1. 3x2在定义域内无界函数,而在[-1,1]内有界:3x2≤3
, 0, , ( ) , ( ) I D M x I f x M f x I 4.有界性:设区间 如果 常数 使得对 有 则称函数 在区间 上有界. 二. 函数的性质 2 2 sin sin 1. 3 1 1 3 3. x x x x 例如: 在定义域内是有界函数: 在定义域内无界函数,而在[- ,]内有界: 单调性、奇偶性、周期性、有界性