
第三章导数与微分 教学要求()理解导数的概念和导数的几何意义,会求平面曲线的切线方程 和法线方程:理解函数的可导与连续性之间的关系:了解高 阶导数的概念 高阶导数 (2课时) ②米提基本初等函数的求导公式,导数的四则运算法则、复 数及隐函数的求导法则。(2课时) (3)理解一元函数微分的概念,理解可微与可导之间的关系,掌握 微分的运算方法,了解微分在近似计算中的应用。(2课时) 教学重点导数的概念及几何意义:导数的四则运算法则、复合函数求导法 则和隐函数求导法:微分的概念 教学难点导数的概念,复合函数、反函数、隐函数求导法则 第一节函数的局部变化率一导数 抽象导数概念的两个现实原型 我们在解决实际问题时,除了需要了解变量之间的函数关系以外,有时还需 要研究变量变化快慢的程度例如物体运动的速度,城市人口增长的速度,国民 经济发展的速度等。其中三类问题导致了微分学的产生: 1:求变速运动的瞬时速度2:求曲线上一点处的切线3:求极大值和极小值 原型】求变速直线运动的瞬时速度 有一质点以O为原点做变速直线运动,用s表示质点运动的路程,s是时间t的 函数,记作s=f),1e0,T可,求。∈0,T门时刻的瞬时速度. 分析:匀速直线运动中=,变速直线运动不能直接用公式,速度的变与不变如 何解决? 解决步骤:(1)求增量:给。一个增量△1,时间从。变到了1=4,+△1,路程增量 △s=f4)-f()=f(+△)-f) (2)求增量比:当△1很小时,质点在该时间段内的运动可近似的看成匀速运 动,则△内的平均速度 =△s=f,+△)-f6) (3)取极限:当△越来越小,平均速度越来越接近于1,时刻的瞬时速度.于 是△1→0时,平均速度的极限就是瞬时速度,即 %产细名 、f(。+)-f) At
1 第三章 导数与微分 教学要求 (1) 理解导数的概念和导数的几何意义,会求平面曲线的切线方程 和法线方程;理解函数的可导与连续性之间的关系;了解高 阶导数的概念,会求简单函数的高阶导数。(2 课时) (2) 掌握基本初等函数的求导公式,导数的四则运算法则、复合函 数及隐函数的求导法则。(2 课时) (3) 理解一元函数微分的概念,理解可微与可导之间的关系,掌握 微分的运算方法,了解微分在近似计算中的应用。(2 课时) 教学重点 导数的概念及几何意义;导数的四则运算法则、复合函数求导法 则和隐函数求导法;微分的概念 教学难点 导数的概念,复合函数、反函数、隐函数求导法则 第一节 函数的局部变化率——导数 一、 抽象导数概念的两个现实原型 我们在解决实际问题时,除了需要了解变量之间的函数关系以外,有时还需 要研究变量变化快慢的程度.例如物体运动的速度,城市人口增长的速度,国民 经济发展的速度等。其中三类问题导致了微分学的产生: 1:求变速运动的瞬时速度 2:求曲线上一点处的切线 3:求极大值和极小值 原型Ⅰ 求变速直线运动的瞬时速度 有一质点以 O 为原点做变速直线运动,用 s 表示质点运动的路程,s 是时间 t 的 函数,记作s ft t = ∈ ( ), [0,T],求 0t ∈[0,T]时刻的瞬时速度. 分析:匀速直线运动中 = s v T ,变速直线运动不能直接用公式,速度的变与不变如 何解决? 解决步骤:(1)求增量:给 0t 一个增量Δt ,时间从 0t 变到了tt t 1 0 = +Δ ,路程增量 10 0 0 Δ = = +Δ s ft ft ft t ft ( )- ( ) ( )- ( ). (2)求增量比:当Δt 很小时,质点在该时间段内的运动可近似的看成匀速运 动,则Δt 内的平均速度 0 0 ( )- ( ) = =s f t t ft v t t Δ + Δ Δ Δ . (3)取极限:当Δt 越来越小,平均速度越来越接近于 0t 时刻的瞬时速度. 于 是Δ →t 0 时,平均速度的极限就是瞬时速度,即 0 0 0 t0 t0 t0 ( )- ( ) = lim = lim = lim s f t t ft v v t t Δ→ Δ→ Δ→ Δ + Δ Δ Δ

原型Ⅱ求曲线切线的斜率 M(x,y)和M(x,y)是曲线y=f(x)上两点,它们的 连线是该曲线的一条割线.当点M沿曲线无限接近 于点M,时,割线绕点M,转动,其极限位置M,T就 是曲线在点M。处的切线(图3.1),求曲线在点M。处 切线的斜率。 分析:若)=)的图像为直线。则斜率=然 y=(x)的图像为曲线,如何用直线的斜率来解决? 和十△r 解决步骤: (1)求增量:给x。一个增量△x,自变量由变到+△x,则 △y寸f(x+△x)-f(x,) (2)求增量比:Ay=f+Ax)f △r △r (》取极限:aa=一是-▣化+a-其中aa受是切线 △ M。T与x轴的夹角 总结:上面两个现实原型的范畴虽不相同,但从纯数学的角度来考察,所要解决 的问题相同:求一个变量相对于另一个相关变量的变化快慢程度,即变化率问题: 处理问题的思想方法相同:矛盾转化的辨证方法:数学结构相同:函数改变量与 自变量改变之比,当自变量改变量趋于零时的极限。由这两个具体问题便可抽 象出导数的概念 二、导数的概念 1.定义:设函数y=f(x)在点x,的某一邻域内有定义,当自变量x在x。处有 增量△x(点x,+△x仍在该邻域内)时,相应地函数有增量Ayf(x+A)-f(), 如果当△→0时,架的樱限存在,则移这个极限值为)y=在点气处的导数, 记作儿,即 儿是+园 (3.1) Ar 也可记作了(G).安或妥 如果极限(3.1)存在,则称函数fx)在点x处可导:如果极限(3.1)不存在, 2
2 原型 II 求曲线切线的斜率 M (, ) x y 和 0 M (, ) x y 是曲线 y = f x( ) 上两点,它们的 连线是该曲线的一条割线.当点 M 沿曲线无限接近 于点M0 时,割线绕点 M0 转动,其极限位置M0 T 就 是曲线在点M0 处的切线(图 3.1),求曲线在点M0 处 切线的斜率. 分析:若 y fx = ( ) 的图像为直线,则斜率 = y k x Δ Δ . y = f x( ) 的图像为曲线,如何用直线的斜率来解决? 解决步骤: (1) 求 增 量 : 给 0 x 一个增量 Δx ,自变量由 0 x 变 到 x0+Δx , 则 = ( )- ( ) 0 0 Δ +Δ y fx x fx (2) 求增量比: 0 0 ( )- ( ) =y f x x fx x x Δ + Δ Δ Δ . (3) 取极限: 0 0 0 0 ( ) () tan lim lim Δ→ Δ→ Δ + Δ − = = x x Δ Δ y f x x f x x x α . 其中 ( ) 2 π α α ≠ 是切线 M0 T 与 x 轴的夹角. 总结:上面两个现实原型的范畴虽不相同,但从纯数学的角度来考察,所要解决 的问题相同:求一个变量相对于另一个相关变量的变化快慢程度,即变化率问题; 处理问题的思想方法相同;矛盾转化的辨证方法;数学结构相同:函数改变量与 自变量改变之比,当自变量改变量趋于零时的极限. 由这两个具体问题便可抽 象出导数的概念。 二、导数的概念 1. 定义: 设函数 y = f x( ) 在点 0 x 的某一邻域内有定义,当自变量 x 在 0 x 处有 增量Δx (点 x0+Δx 仍在该邻域内)时,相应地函数有增量 = ( )- ( ) 0 0 Δy fx x fx + Δ , 如果当Δ →x 0时, y x Δ Δ 的极限存在,则称这个极限值为 y fx = ( ) 在点 0 x 处的导数, 记作 = 0 ' x x y ,即 0 0 0 0 0 ( )- ( ) ' | = lim = lim x x x x y f x x fx y x x = Δ→ Δ→ Δ + Δ Δ Δ . (3.1) 也可记作 0 f ' ( ) x , = 0 x x dy dx 或 = 0 ( ) x x d f x dx . 如果极限(3.1)存在,则称函数 f ( ) x 在点 0 x 处可导;如果极限(3.1)不存在

则称函数f(x)在点x,处不可导. 注:0.密表示导数的一个整体行号。 (②).导数是平均变化率的极限!导数的力学意义是变速直线运动物体的瞬时 速度:导数的几何意义是曲线切线的斜率。 2.求导数步骤与例题: (1)给x一个增量△x,则函数增量△f(x+A-f(x月 (2)求平均变化率y-f伍+Af): △r 3))求平均变化幸的极限儿-四是回 △x 例1.求函数f(x)C(常数)在x,点的导数 解:)=+Af_CC-0.即常数的导数为零 △r △r 例2.求函数f(x)=x在点x=2的导数. 解:给x=2一个增量△x,则函数增量为△y=(2+△x)2-2=4△r+(△x)2.平均变化 率为袋4+于是)-是-四4+a=4 Ar 说明:如果函数y=f(x)在区间(a,b)内的每一点处都可导,则称函数y=f(x)在 区间(a,b)内可导,且称f(x)为函数y=fx)的导函数.显然函数y=fx)在点 x,处的导数f(x),就是导函数∫(x)在x处的函数值,即∫(x)=∫(x) 例3.求函数)=在x处的导数. 解:先求导函数。给任意一点x一个增量A,得到A+Axx+A) 11-△x 所以y=巴是-把A子再求处的导数(礼引 -1 例4.求函数y=√F的导数 解:任取一点x∈(0,+o)一个增量△x,得到△y=√+△x-√F 是 1 ArVx+△r+V 所以y=四然=+xG2g 说明:由前面的三个例子发现,幂函数的导数公式(xy=ax(a为任一实数) 3
3 则称函数 f ( ) x 在点 0 x 处不可导. 注:(1). dy dx 表示导数的一个整体符号. (2).导数是平均变化率的极限!导数的力学意义是变速直线运动物体的瞬时 速度;导数的几何意义是曲线切线的斜率. 2. 求导数步骤与例题: (1) 给 0 x 一个增量Δx ,则函数增量 = ( )- ( ) 0 0 Δy fx x fx + Δ ; (2) 求平均变化率 0 0 ( )- ( ) =y f x x fx x x Δ + Δ Δ Δ ; (3) 求平均变化率的极限 0 0 0 0 0 ( )- ( ) ' | = lim = lim x x x x y f x x fx y x x = Δ→ Δ→ Δ + Δ Δ Δ . 例 1. 0 求函数 常数 在 点的导数 fx x ( )=C( ) . 解: 0 0 0 0 ( ) () - ( ) lim = =0 x fx x fx C C f x Δ → x x +Δ − ′ = Δ Δ . 即常数的导数为零. 例 2. 2 求函数 在点 的导数 fx x x ( )= 2 . = 解:给 x = 2一个增量Δx ,则函数增量为 22 2 Δ +Δ = Δ + Δ y=(2 ) -2 4 ( ) . x xx 平均变化 率为 =4+ , y x x Δ Δ Δ 于是 0 0 '(2) lim lim (4 ) 4. x x y f x Δ→ Δ→ x Δ = = +Δ = Δ 说明:如果函数 y = f x( ) 在区间(,) a b 内的每一点处都可导,则称函数 y = f x( ) 在 区间(,) a b 内可导,且称 f '( ) x 为函数 y = f x( ) 的导函数. 显然函数 y = f x( ) 在点 0 x 处的导数 0 f '( ) x ,就是导函数 f '( ) x 在 0 x 处的函数值,即 0 0 '( ) '( ) x x fx fx = = . 例 3.求函数 1 y= x 在 x=1处的导数. 解:先求导函数. 给任意一点 x 一个增量Δx ,得到 11 - = -= . + () x y x x x xx x Δ Δ Δ + Δ . 所以 2 0 0 -1 1 ' lim lim - . ( ) x x y y Δ→ Δ→ x xx x x Δ == = Δ +Δ 再求 x=1处的导数 =1 =1 2 1 ' ( - )| =-1. x x y x = 例 4. 求函数 y= x 的导数. 解:任取一点 x∈ ∞ (0,+ ) 一个增量Δx ,得到Δ Δ y=+- xx x - 1 == . + y x xx x x x x x Δ +Δ Δ Δ + Δ 所以 0 0 1 1 ' lim lim . + 2 x x y y x x xx x Δ→ Δ→ Δ == = Δ + Δ 说明:由前面的三个例子发现,幂函数的导数公式 -1 ( )' ( ) x x α α =α α为任一实数

同理,我们还可以证明 1 3、左导数与右导数 (1)求函数y=fx)在点x。处的导数时,x→x,的方式是任意的。如果x仅从x 之左趋于。,记作x→x,或△r→0,若此时y极限存在,则称该极限值叫 做函数)=在点气的左导数,记作∫-化,即了-(化广是同理有右 号数了,化)广册:,其中△→0广表示从x右侧趋于元 (2)函数在一点处的左、右导数与函数在该点处可导之间的关系 定理:函数y=f(x)在点x,可导的充分必要条件是函数y=(x)在点x,处的左 右导数存在且相等。 例:函数f(x)x在点x,=0处不可导. 解给气=0一个增量△0,则闲应的有左号数了-化广一是-一是= 同强,给6=0一个增量40,相应的右导数为八化广一是一会铝 即f(0)≠(0),故函数(x)x在点x=0处不可导. 三、函数的连续性与可导的关系 定理:如果函数y=f(x)在点x,处可导,那么y=f(x)在点x处连续. 该定理可可简术为:可导叫连续 说明:1.由可导的定义,变量、极限和无穷小量的关系定理可以证明 △r→0时,y=y'△r+ax→0 2.该定理的逆命题并不成立.如f(x)=x在点x,=0处连续但不可导. 四、高阶导数 因为y-f(x)的导函数f(x)也是x的导数,我们把函数y=f(x)的导数f'(x)的 导数(x)叫做函数的二阶导数,记作y,也可记作 减安其中空县密 二阶导数的力学意义是运动物体的加速度. 二阶导数的导数称为三阶导数。记作"《x)减 dx 设函数y=f(x)的存在n-1阶导数,且-1阶导数可导,那么y=f(x)的n-1阶
4 同理,我们还可以证明 1 1 (sin )' cos . (cos )' -sin . (log )' . (ln )' . ln a x xx x x x x a x = = == 3、左导数与右导数 (1)求函数 y fx = ( ) 在点 0 x 处的导数时, 0 x → x 的方式是任意的。如果 x 仅从 0 x 之左趋于 0 x ,记作 0 x → x -,或 - Δ →x 0 ,若此时 y x Δ Δ 极限存在,则称该极限值叫 做函数 y = f x( ) 在点 0 x 的左导数,记作 0 f ' _ ( ) x ,即 0 - 0 ' _ ( )= limx y f x Δ → x Δ Δ .同理有右 导数 + 0 + 0 ' ( )= limx y f x Δ → x Δ Δ ,其中 + Δ →x 0 表示从 0 x 右侧趋于 0 x . (2)函数在一点处的左、右导数与函数在该点处可导之间的关系 定理:函数 y fx = ( ) 在点 0 x 可导的充分必要条件是函数 y fx = ( ) 在点 0 x 处的左、 右导数存在且相等。 例:函数 f () | | x x = 在点 x0=0 处不可导. 解:给 x0=0 一个增量Δx<0,则相应的有左导数 0 - - 0 0 - ' _ ( )= lim = lim =-1. x x y x f x Δ→ Δ→ x x Δ Δ Δ Δ 同理,给 x0=0 一个增量Δx>0,相应的右导数为 + 0 + + 0 0 ' ( )= lim = lim =1. x x y x f x Δ→ Δ→ x x Δ Δ Δ Δ f f (0) (0), + − 即 ′ ′ ≠ 故函数 f () | | x x = 在点 x0=0 处不可导. 三、函数的连续性与可导的关系 定理:如果函数 y fx = ( ) 在点 0 x 处可导,那么 y fx = ( ) 在点 0 x 处连续. 该定理可简述为:可导则连续. 说明:1. 由可导的定义,变量、极限和无穷小量的关系定理可以证明 Δ →x 0时,Δyyx x = Δ+ Δ→ ' 0 α 2. 该定理的逆命题并不成立. 如 f () | | x x = 在点 x0=0 处连续但不可导. 四、高阶导数 因为 y = f x( ) 的导函数 f '( ) x 也是 x 的导数,我们把函数 y = f x( ) 的导数 f '( ) x 的 导数[ '( )]' f x 叫做函数的二阶导数,记作 y'' ,也可记作 2 2 2 2 ''( ) , = ( ). 或 其中 d y d y d dy f x dx dx dx dx 二阶导数的力学意义是运动物体的加速度. 二阶导数的导数称为三阶导数, 记作 3 3 '''= '''( ) . 或 d y yf x dx 设函数 y fx = ( ) 的存在 n-1 阶导数,且 n-1 阶导数可导,那么 y fx = ( ) 的 n-1 阶
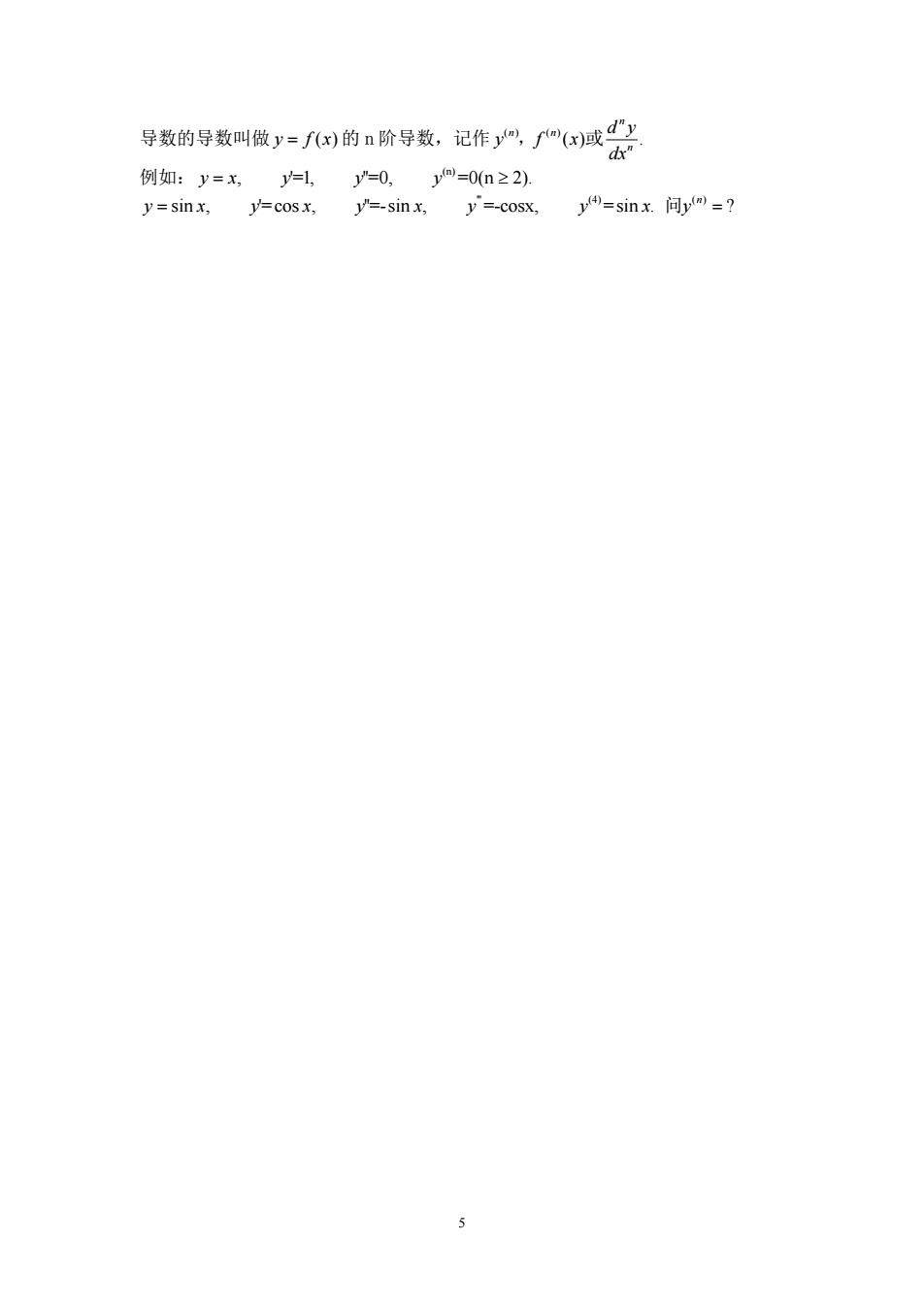
导数的导数叫做y=f)的n阶导数,记作%,了(x减以 例如:y=x,y=l,y=0,ym=0n≥2). y=sinx,y=cosx, y=-sinx,y'=-cosx y9=sinx.问ym=?
5 导数的导数叫做 y fx = ( ) 的 n 阶导数,记作 () () , 或 () . n n n n d y y fx dx 例如: (n) yx y y y = ≥ , '=1, ''=0, =0(n 2). ''' (4) ( ) sin , '= cos , ''=-sin , =-cosx, =sin . ? 问 n y x y x y x y y xy = =