
第四章导数的应用问题 4.1中值定理 4.2洛必达法则 4.3函数的单调性与极值
第四章 导数的应用问题 4.1 中值定理 4.2 洛必达法则 4.3 函数的单调性与极值
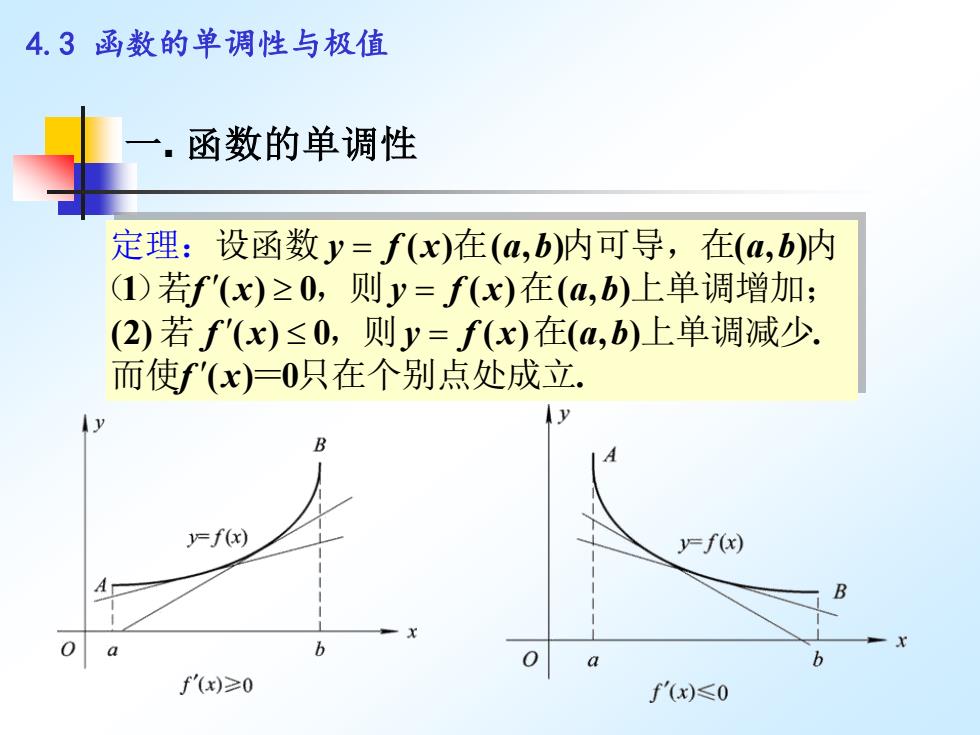
4.3函数的单调性与极值 函数的单调性 定理:设函数y=f(x)在(a,b)内可导,在(a,b)内 (I)若f'(x)≥0,则y=f(x)在(a,b)上单调增加; (2)若f'(x)≤0,则y=f(x)在(a,b)上单调减少. 而使f'(x)=0只在个别点处成立. y y B f(x) y=f(x) B b 6 f'(x)≥0 f'(x)≤0
4.3 函数的单调性与极值 ( ) ( , ) ( , ) 1 ( ) 0 ( ) ( , ) (2) ( ) 0 ( ) ( , ) . ( ) 0 . y f x a b a b f x y f x a b f x y f x a b f x = = = 设函数 在 内可导,在 内 ( )若 ,则 在 上单调增加; 若 ,则 定理: 在 上单调减少 而使 = 只在个别点处成立 一. 函数的单调性

4.3函数的单调性与极值 说明: 1.上述定理的证明,可以由中值定理得到, f(x2)-f(x)=f'(5)x2-x1) (x1<5<x2) 2.一般的,我们用驻点('(x)=0)将区间分成几个子区 间,在这些子区间上判定函数的单调性。 例题1 讨论函数f(x)=(x-1)2-4的单调性 解f(x)的定义域是(-o0,+∞),f'(x)=2(x-1)=0 得驻点x=1.当x<1时,f'(x)<0,当x>1时,'(x)>0. ∴.f(x)的单减区间是(-o,1),f(x)的单增区间是(L,+o)
4.3 函数的单调性与极值 2 1 2 1 1 2 1. f x f x f x x x x ( ) ( ) ( )( ) ( ) − = − 上述定理的证明,可以由中值定理得到. ( ) (- , ), '( ) 2( -1) 0 1. 1 '( ) 0; 1 '( ) 0. + = = = 解 的定义域是 得驻点 当 时, 当 时, f x f x x x x f x x f x 2 讨论函数f x x ( ) ( 1) - 4 . = − 的单调性 说明: 2. 一般的,我们用驻点 ( )将区间分成几个子区 间,在这些子区间上判定函数的单调性。 f x'( ) 0 = 例题1 + f x f x ( ) (- ,1), ( ) (1, ). 的单减区间是 的单增区间是
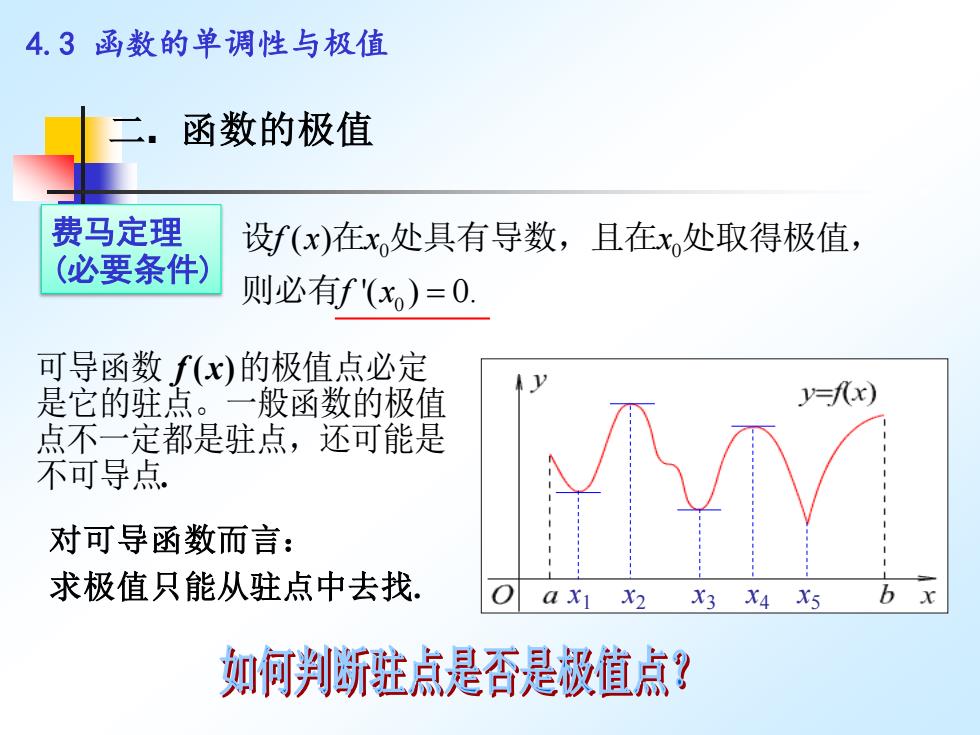
4.3函数的单调性与极值 函数的极值 费马定理 设f(x)在x处具有导数,且在x处取得极值, (必要条件) 则必有f'(x)=0. 可导函数f(x)的极值点必定 是它的驻点。一般函数的极值 y=fx) 点不一定都是驻点,还可能是 不可导点. 对可导函数而言: 求极值只能从驻点中去找: a X1 X2 X3 X4 X5 b x 如何判断驻点是否是值点?
4.3 函数的单调性与极值 二. 函数的极值 费马定理 (必要条件) x1 x2 x3 x4 x5 ( ) . 可导函数 的极值点必定 是它的驻点。一般函数的极值 点不一定都是驻点,还可能是 不可导点 f x 对可导函数而言: 求极值只能从驻点中去找. 0 0 0 ( ) '( ) 0. f x x x f x = 设 在 处具有导数,且在 处取得极值, 则必有

4.3函数的单调性与极值 1.判别法则I f(x)在x的邻域可导且f'(xo)=0 (1) 如果在x的左侧有f'(x)<0,在x的右侧有f'(x)>0,则f(x) 在x处取得极小值 (2)如果在x的左侧有f'(x)>0,在x,的右侧有f'(x)<0,则f(x) 在x,处取得极大值 (3)如果在x的左右两侧有f(x)符号相同,则f(x)在x处没有极值 '(x0)=0 x0)>0 Kx0)>0 (x0)K0 f()0 f'(xo)=0 0 x0 xo
4.3 函数的单调性与极值 f (x)在x0 的邻域可导且f '(x0 ) = 0 1. 判别法则I 0 0 0 '( ) 0 '( ) 0 ( ) . x f x x f x f x x (1) 如果在 的左侧有 ,在 的右侧有 ,则 在 处取得极小值 0 0 0 '( ) 0 '( ) 0 ( ) . x f x x f x f x x (2) 如果在 的左侧有 ,在 的右侧有 ,则 在 处取得极大值 0 0 (3) 如果在x f x f x x 的左右两侧有 '( ) ( ) . 符号相同,则 在 处没有极值