
第2章微积分的直接基础一函数 §2.1数列极限与函数极限 §2.2极限的性质与运算 §2.3连续函数
第2章微积分的直接基础——函数 §2.1 数列极限与函数极限 §2.2 极限的性质与运算 §2.3 连续函数
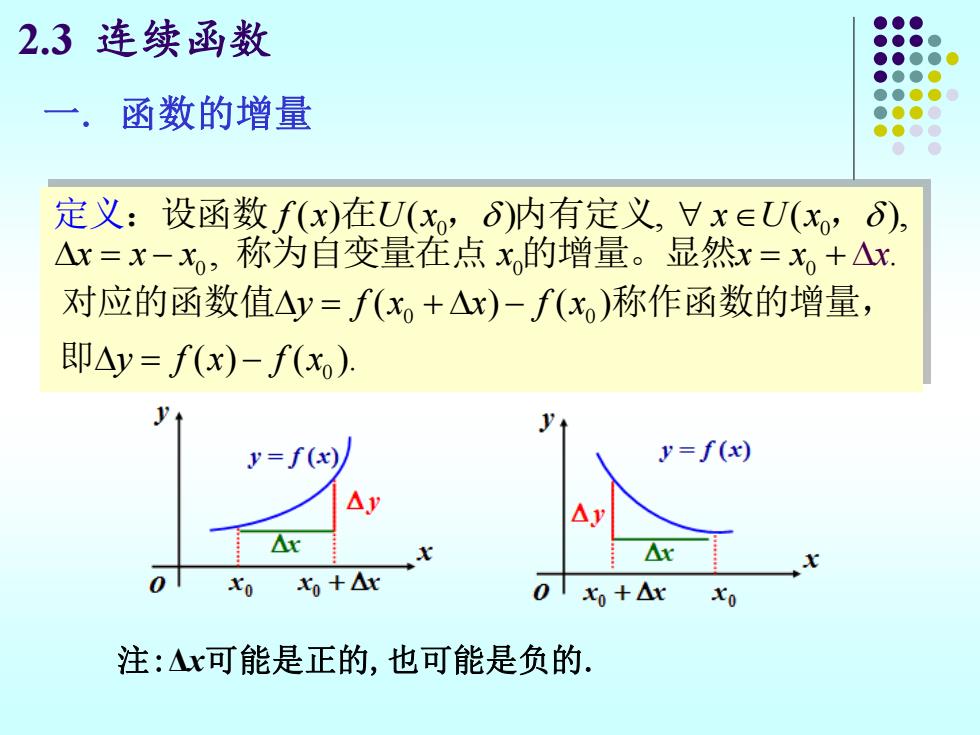
2.3连续函数 一.函数的增量 定义:设函数f(x)在U(x,δ)内有定义,Vx∈U(x,δ), △x=x-x,称为自变量在点x的增量。显然x=x,+△x 对应的函数值△y=f(x,+△x)-f(x)称作函数的增量, 即△y=f(x)-f(xo). y=f(x) y=f(x) △ △y △ △( xo 0+△r 01x+△x 注:△x可能是正的,也可能是负的
2.3 连续函数 一. 函数的增量 0 0 0 0 0 ( ) ( ) , ( ), , . f x U x x U x x x x x x x x = − = + :设函数 在 , 内有定义 , 称为自变量在点 的增 然 义 量。显 定 0 0 0 ( ) ( ) ( ) ( ). y f x x f x y f x f x = + − = − 对应的函数值 称作函数的增量, 即 注:Δx可能是正的,也可能是负的

2.3连续函数 ,函数的增量 例如:求函数y=x2+1在x点的增量 给增量△x,x=x+△x, Ay=f(x+△x)-f(x)=(x+△x)2-x2 =2x△x+(△x)2 练习:求函数y=上在x,(X,≠0)点的增量
2.3 连续函数 一. 函数的增量 2 0 例如:求函数y x x = +1 . 在 点的增量 0 给增量 = + x x x x , , 2 2 0 0 0 = + − = + − y f x x f x x x x ( ) ( ) ( ) 2 0 = + 2 ( ) x x x 0 0 1 y x x( 0) . x 练习:求函数 = 在 点的增量

2.3连续函数 二。 连续函数的定义 定义1设函数f(x)在U(x,δ)内有定义,如果 当自变量的增量△x趋向于O时,对应的函数 增量△y也趋向于0,即lim△y=0, △x>0 或lim[f(x+△x)f(x】=0,那么就称函数 0 f(x)在点x连续,也称x是f(x)连续点. 说明:1.连续函数的自变量变化很小时,函数值的变化也很小 2.图像上看,连续函数是一条连续而不间断的曲线
2.3 连续函数 0 0 0 0 0 0 0 ( , ) , 0 0 lim 0 lim[ ] 0 x x f x U x x y y f x x f x f x x x f x → → = + = 设函数( )在 内有定义 如果 当自变量的增量 趋向于 时,对应的函数 增量 也趋向于 ,即 , 或 ( )-( ) ,那么就称函数 ( )在点 连续 定义1 ,也称 是( )连续点. 二. 连续函数的定义 说明: 1. 连续函数的自变量变化很小时,函数值的变化也很小. 2.图像上看,连续函数是一条连续而不间断的曲线

2.3连续函数 连续函数的定义 定义2 设函数f(x)在U(x,δ)内有定义,如果 当x→x时,f(x)的极限存在且等于f(x),即 limf(x)=f(x),那么就称f(x)在点x,连续 说明:定义1与定义2是等价的, 定义1 lim Ay=0limf(x+Ax)-f(xa)=0 △x→0 台mf(化,+△e)=fx)台limf(x)=fx,) 定义2
2.3 连续函数 二. 连续函数的定义 0 0 0 0 0 0 ( ) ( , ) , ( ) ( ) lim ( ) ( ) ( ) . x x f x U x x x f x f x f x f x f x x → → = 设函数 在 内有定义 如果 当 时, 的极限存在且 定 等于 ,即 ,那么就称 在点 2 连续 义 0 lim 0 x y → = 0 0 0 lim ( ) ( ) 0 x f x x f x → + − = 说明: 定义1与定义2是等价的. 0 0 0 lim ( ) ( ) x f x x f x → + = 0 0 lim ( ) ( ) x x f x f x → = 定义1 定义2