
(0) (0) (0) (0) r A- a a a4ia g (r=2,3,…,n) r d) 则A的r阶顺序主子式△,=a9a…a,》a,若△,≠0,则an≠0 可定义c, 并构造Frobenius矩阵 6
(0) (0) (0) (0) 11 1 1 1 1 ( 2) ( 2) ( 2) ( 1) 11 1 1 ( 1) ( 1) ( 1) ( 1) rr n rr r r rr rr r n r r rr rn r r nr nn a aa a aa a A a a a a − −− − − −− − − − − − − = ( 2,3, , ) r n = 则 A 的 r 阶顺序主子式 (0) (1) ( 2) 1 11 22 1 1 r r r r r rr aa a a − − ∆ = − − ,若 0 ∆ ≠ r ,则 1 0 r rr a − ≠ 可定义 1 1 r ir ir r rr a c a − − = ,并构造 Frobenius 矩阵 6
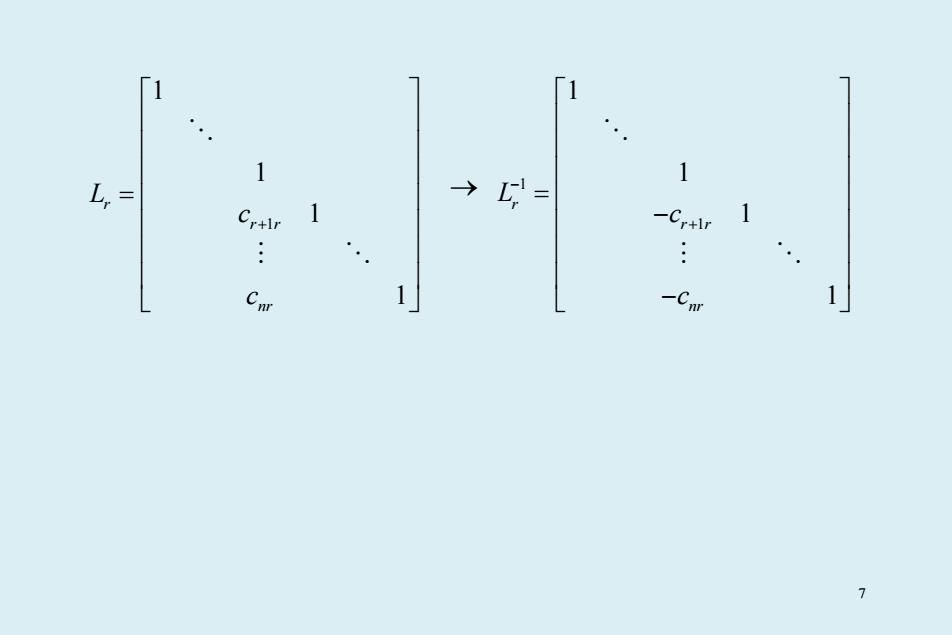
1 1 1 L, → = C 1 -Cr+lr 1 : .: C 1」 -Cnr 1 7
1 1 1 1 1 r r r nr L c c + = → 1 1 1 1 1 1 r r r nr L c c − + = − − 7
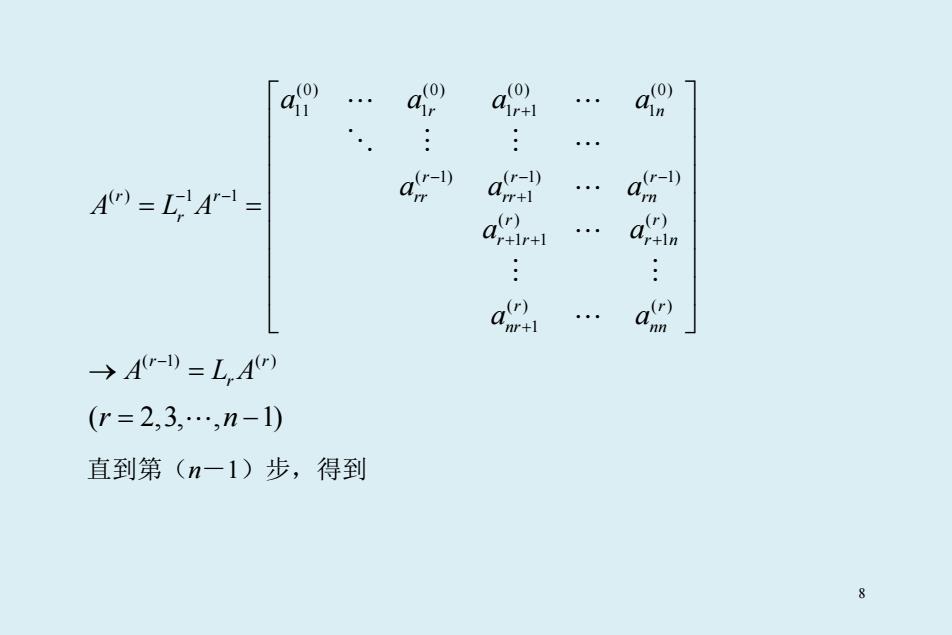
a a (0) (0) A()=L.A"-= q() r+1r+1 a) r+ln →A-)=L,A) (r=2,3,…,n-1) 直到第(n一1)步,得到 8
(0) (0) (0) (0) 11 1 1 1 1 ( 1) ( 1) ( 1) () 1 1 1 ( ) ( ) 1 1 1 ( ) ( ) 1 rr n rr r r r rr rr rn r r r r r r n r r nr nn a aa a aa a A LA a a a a + −− − − − + + + + + = = → ( 1) ( ) r r A LA r − = ( 2,3, , 1) r n = − 直到第(n-1)步,得到 8