
第二十讲矩阵特征值估计
第二十讲 矩阵特征值估计 1

特征值计算较困难,希望找到简便的特征值界限或分布范围的估 计方法。 一、特征值界的估计 定理1.设A∈R”,入为A的任意特征值,则有 im 其中,M=max ay-an I<i,j<n 2 证明:设x为A的属于特征值几的单位特征向量,即Ax=x,xHx=1, 则 2
特征值计算较困难,希望找到简便的特征值界限或分布范围的估 计方法。 一、 特征值界的估计 定理 1. 设 n n A R × ∈ ,λ为 A 的任意特征值,则有 ( ) ( 1) Im 2 n n λ M − ≤ 其中, 1 i,j n max 2 ij ji a a M ≤ ≤ − = 证明:设 x 为 A 的属于特征值λ的单位特征向量,即 Ax x = λ , 1 H x x = , 则 2
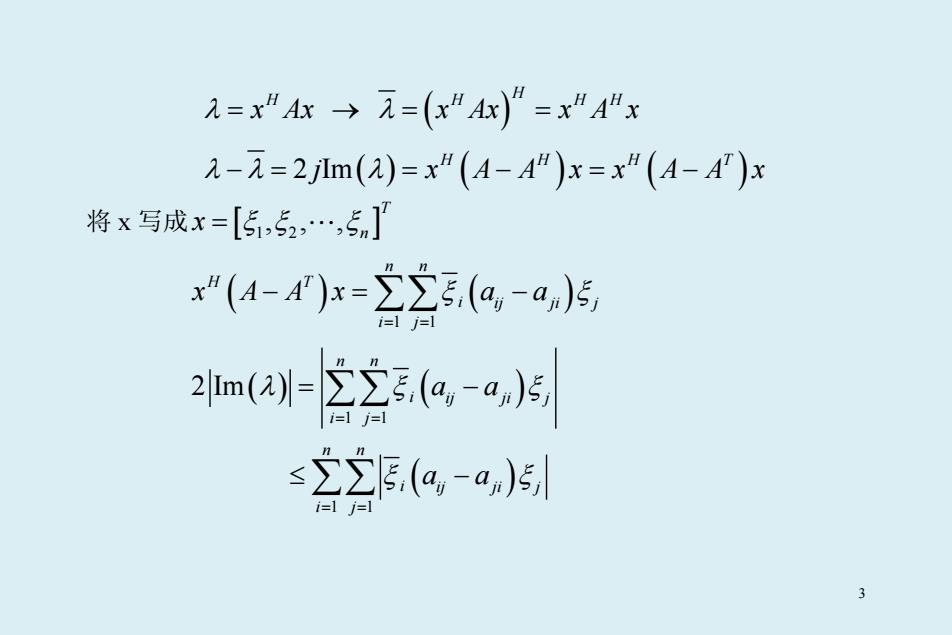
=x”A→元=(x”A)=x”Ax -元=2lm(2)=x”(A-A)x=x“(A-A)x 将x写成x=[5,52,…,5n] x(4-4)x=∑∑,(a,-a)5 2m(2-2空a,-a,片 ≤2∑E.(a,-a)5 3
H λ = x Ax → ( ) H H H H λ = = x Ax x A x 2 Im( ) ( ) ( ) H HH T λλ λ −= = − = − j x AA xx AAx 将 x 写成 [ 1 2 ,,, ] T n x = ξξ ξ ( ) ( ) 1 1 n n H T i ij ji j i j x AAx a a ξ ξ = = −= − ∑∑ ( ) ( ) ( ) 1 1 1 1 2 Im n n i ij ji j i j n n i ij ji j i j a a a a λξ ξ ξ ξ = = = = = − ≤ − ∑∑ ∑∑ 3
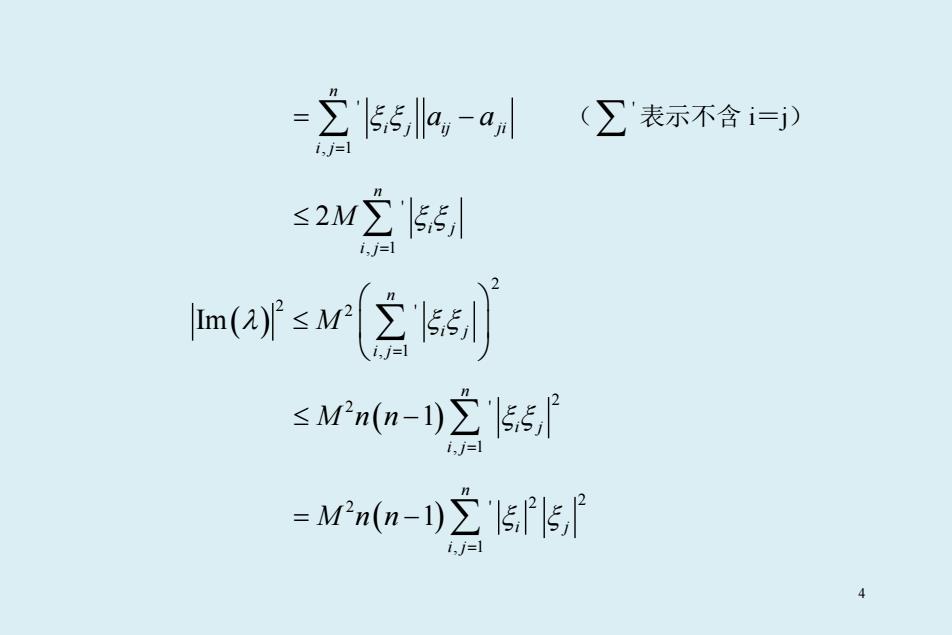
=∑5,-a(∑表示不含=D s2w空5 m(afsr含15 ≤Mn(n-)∑'ls5f =M2n(n-)∑'l515,f 4
' , 1 n i j ij ji i j ξ ξ a a = = ∑ − ( ' ∑ 表示不含 i=j) ' , 1 2 n i j i j M ξ ξ = ≤ ∑ ( ) 2 2 2 ' , 1 Im n i j i j λ M ξ ξ = ≤ ∑ ( ) 2 2 ' , 1 1 n i j i j Mnn ξ ξ = ≤ − ∑ ( ) 2 2 2 ' , 1 1 n i j i j Mnn ξ ξ = = − ∑ 4
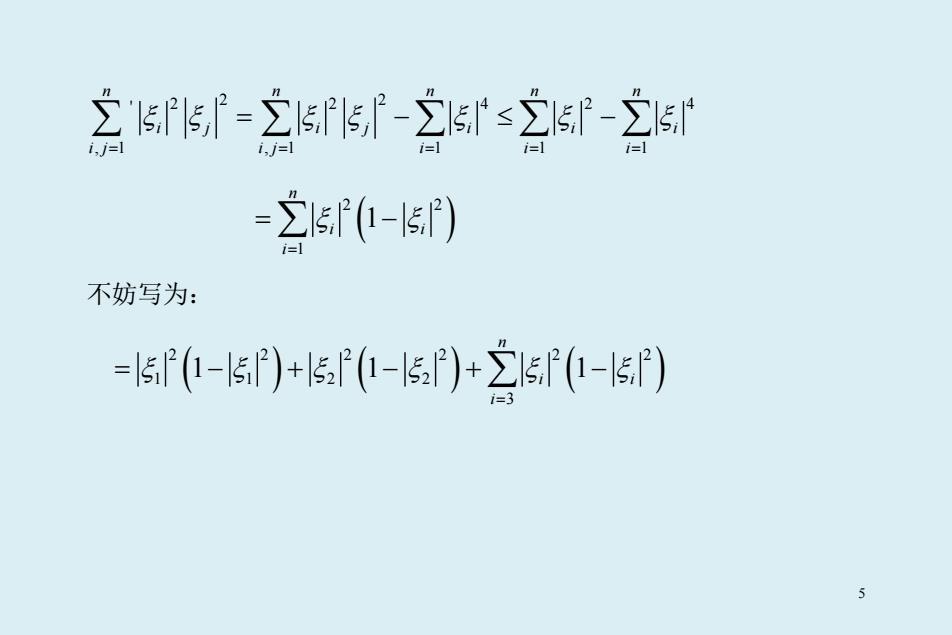
之5f-2f-sf-立 =-) 不妨写为: =(-5)+5a(-)+(-)
2 2 424 2 2 ' , 1 , 1 1 1 1 n n nnn ij ij i i i i j i j i i i ξξ ξξ ξ ξ ξ = = = = = ∑ ∑ ∑∑∑ = −≤− ( ) 2 2 1 1 n i i i ξ ξ = = − ∑ 不妨写为: ( ) ( ) ( ) 2 22 2 2 2 1 12 2 3 11 1 n i i i ξ ξξ ξ ξ ξ = = −+ −+ − ∑ 5