
定理2若F(x)是f(x)的一个原函数,则f(x)的所有 原函数都在函数族F(x)+C(C为任意常数)内. 证:1)(F(x)+C)}=F'(x)=f(x) ∴.F(x)+C是f(x)的原函数 2)设D(x)是f(x)的任一原函数,即 Φ'(x)=f(x) 又知 F'(x)=f(x) .[Φ(x)-F(x)]'=Φ'(x)-F'(x)=f(x)-f(x)=0 故 ①(x)=F(x)+Co(C0为某个常数) 即①(x)=F(x)+C属于函数族F(x)+C. 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 是若 xfxF )()( 的一个原函数, 则 xf )( 的所有 原函数都在函数族 )( + CxF ( C 为任意常数 ) 内 . 证 : 1) ∴ + 是 xfCxF )()( 的原函数 ∵ + CxF ))(( ′= ′ xF )( = f x)( Φ 是设 xfx )()()2 的任一原函数, Φ′ x = f x)()( 又知 F′ x = f x)()( ∴ Φ − xFx ])()([ ′= Φ′ − ′ xFx )()( = f x − f x = 0)()( 故 0 Φ = )()( + CxFx ( ) C 0 为某个常数 即 0 Φ x = F x)()( + C 属于函数族 Fx C () . + 即 定理 2

定义2f(x)在区间I上的原函数全体称为f(x)在1 上的不定积分,记作∫f(x)dx,其中 ∫一积分号;f)一被积函数; x一积分变量;f(x)dx一被积表达式. 若F'(x)=f(x),则 f(x)dx=F(x)+C(C为任意常数) 例如,「edx=e+C C称为积分常数 ∫x2dr=x3+C 不可丢! sin xdx=-cosx+C 2009年7月3日星期五 8 目录 上页 下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 f x)( 在区间 I 上的原函数全体称为 )( 在Ixf 上的不定积分, xxf ,d)( ∫ 其中 ∫ — 积分号 ; f x)( — 被积函数 ; x — 积分变量 ; f d)( xx — 被积表达式 . 若 F′ x = f x ,)()( 则 += CxFxxf ∫ )(d)( ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如 , = ∫ xex d Cex + = ∫ dxx2 + Cx3 3 1 = ∫ dsin xx − cos x + C 记作 定义 2
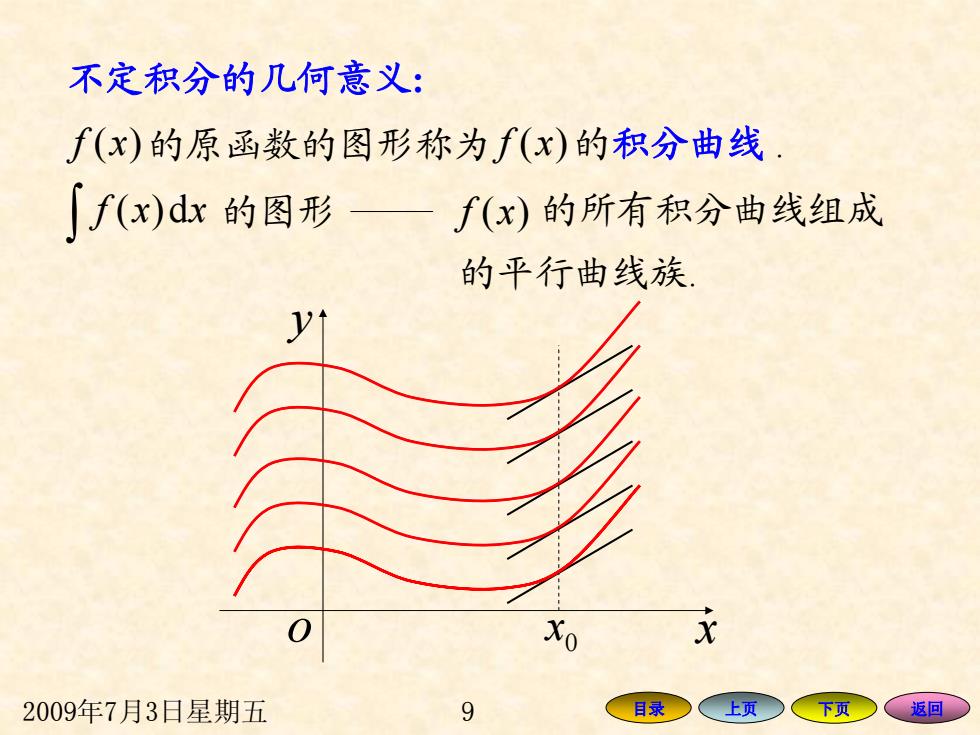
不定积分的几何意义: f(x)的原函数的图形称为f(x)的积分曲线 ∫f(x)dr的图形一f(x)的所有积分曲线组成 的平行曲线族, Xo 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 f x)( 的原函数的图形称为 f x)( d)( xxf ∫ 的图形 f x)( 的所有积分曲线组成 的平行曲线族. y o x 0 x 的积分曲线 . 不定积分的几何意义 :