
第一章函数与极限 5 (2)y=x+lnx,(0,+) 证(1)y=0=产-1+-x(-, 设1<x2<1.因为 )-。00>0 1 所以(x2)>八x1),即f(x)在(-∞,1)内单调增加. (2)y=f(x)=x+Inx,(0.+). 设0<x1<x2因为 f2)-x)=2+ln-1-ln1=2-+ln>0, 所以f八x2)>(x1),即f(x)在(0,+)内单调增加. 巴5.设f(x)为定义在(-1,)内的奇函数,若f(x)在(0,)内单调增加,证明f(x)在 (-L,0)内也单调增加. 证设-1<x1<x2<0,则0<-x2<-x1<l,由f八x)是奇函数,得/x2)-f(x1)= -八-x2)+f八-x).因为f(x)在(0,)内单调增加,所以八-x1)-f(-x2)>0,从而 f(x2)>f(x1),即f(x)在(-1,0)内也单调增加. 巴6.设下面所考虑的函数都是定义在区间(-1,)上的.证明: (1)两个偶函数的和是偶函数,两个奇函数的和是奇函数: (2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函 数的乘积是奇函数. 证(1)设人(x),2(x)均为偶函数,则(-x)=(x),2(-x)=5(x) 令F(x)=(x)+3(x),于是 F(-x)=(-x)+2(-x)=f(x)+5(x)=F(x), 故F(x)为偶函数. 设g1(x),52(x)均为奇函数,则g1(-x)=-g1(x),82(-x)=-g2(x).令 G(x)=1(x)+g(x),于是 G(-x)=g1(-x)+62(-x)=-g1(x)-g2(x)=-G(x) 故G(x)为奇函数. (2)设(x)2(x)均为偶函数,则(-x)=1(x),2(-x)=5(x).令F(x)= (x)·2(x).于是 F(-x)=1(-x)·2(-x)=(x)52(x)=F(x), 故F(x)为偶函数 设61(x),2(x)均为奇函数,则81(-x)=-1(x),g2(-x)=-2(x).令 G(x)=g1(x)·2(x).于是 G(-x)=g1(-x)·g2(-x)=[-g1(x)][-g2(x)]

6 一、《高等数学》(第七版)上册习题全解 =g1(x)·g2(x)=G(x), 故G(x)为偶函数. 设f(x)为偶函数,g(x)为奇函数,则f(-x)=(x),g(-x)=-g(x)令Hx)= f(x)·g(x),于是 H(-x)=f(-x)·g(-x)=f八x)[-g(x)] =-f八x)·g(x)=-H(x) 故H(x)为奇函数. 四7.下列函数中哪些是偶函数,哪些是奇函数,哪些既非偶函数又非奇函数 (1)y=x2(1-x2); (2)y=3x2-x3: (4)y=x(x-1)(x+1): (5)y=sin x-cos x+1; (6)y=+a 2 解(1)y=f(x)=x2(1-x2),因为 f八-x)=(-x)2[1-(-x)2]=x2(1-x2)=fx) 所以f(x)为偶函数. (2)y=f(x)=3x2-x3,因为 f(-x)=3(-x)2-(-x)3=3x2+x3, f八-x)≠f(x),且f-x)≠-f(x), 所以(x)既非偶函数又非奇函数, 8周为 所以(x)为偶函数. (4)y=f(x)=x(x-1)(x+1),因为 f(-x)=(-x)[(-x)-1][(-x)+1] =-x(x+1)(x-1)=-f八x), 所以f(x)为奇函数 (5)y=f(x)=sinx-cosx+1,因为 f(-x)sin (-x)-cos (-x)+1=-sin x-cosx+1, f八-x)≠f八x)且f八-x)≠-八x), 所以(x)既非偶函数又非奇函数 《Oy=)=”二,因为-)==),所以到为偶函数 2 8。下列各函数中哪些是周期函数?对于周期函数,指出其周期 (1)y=cos(x-2): (2)y=c0s4x: (3)y=1+sin mx; (4)y=xcos x:

第一章函数与极限 7 (5)y=sin2 x. 解(1)是周期函数,周期1=2π (2)是周期函数,周期1=号 (3)是周期函数,周期1=2. (4)不是周期函数. (5)是周期函数,周期1=π 四9.求下列函数的反函数: (1)y=√x+1: 2) (3)y-89ad-k≠0): (4)y=2sim3x-石≤x≤g}: (5)y=1+ln(x+2): (6)y=2*可 2 分析函数∫存在反函数的前提条件为::D一→(D)是单射.本题中所给出的各函 数易证均为单射,特别(1),(4)、(5)、(6)中的函数均为单调函数,故都存在反函数 解(1)由y=x+1解得x=y-1,即反函数为y=x3-1 (2)由y部得出号即反两数为y (3)由y部得=即反两数为y= (4)由y=2sin3x(-石≤x≤石)解得x=号aresin之,即反函数为 (5)由y=1+ln(x+2)解得x=e-1-2,即反函数为y=e-1-2. (6)由了部得=亡,甲反两数为y产 四10.设函数f八x)在数集X上有定义,试证:函数(x)在上有界的充分必要条件是 它在X上既有上界又有下界. 解设八x)在X上有界,即存在M>0,使得 If(x)I≤M,x∈X, 故 -M≤f(x)≤M,xeX, 即f(x)在X上有上界M,下界-M. 反之,设x)在X上有上界K,下界K2,即 K2≤八x)≤K,x∈X

8 一、《高等数学》(第七版)上册习题全解 取M=max IK,I,1K21,则有 f(x)I≤M,xeX, 即f(x)在X上有界. 四11.在下列各题中,求由所给函数构成的复合函数,并求这函数分别对应于给定自 变量值x1和2的函数值: ()y=2,u=sin4=石3=7 (2)y=sn,u=2==年 (3)y=Va,u=1+x2,x1=1,x2=2; (4)y=e“,4=x2,x1=0,x2=1; (5)y=w2,u=e,x1=1,x2=-1. 解(0)y=n子为县 2yn2=号l (3)y=1+x2,y1=2,y2=5. (4)y=e2m=1,n=e (5)y=e2,y1=e2,y2=e-2. 四12.设八x)的定义域D=[0,1],求下列各函数的定义域: (1)f(x2); (2)f(sin x); (3)f(x+a)(a>0): (4)f八x+a)+f(x-a)(a>0). 解(1)0≤x2≤1→x∈[-1,1]. (2)0≤sinx≤1→xe[2nr,(2n+1)π],neZ. (3)0≤x+a≤1→xe[-a,1-a]. (40sr+as1, l0≤x-a≤1 →当0<a≤2时xe[a,l-a]:当a>2时,定义域为0. 四13.设 r1,1xl<1. f(x)=0.Ixl=1.g(x)=e', 「-1,1x>1, 求爪g(x)]和g[f(x)],并作出这两个函数的图形. 1,x<0, 解 f[g(x)]=fe)={0,x=0 -1,x>0
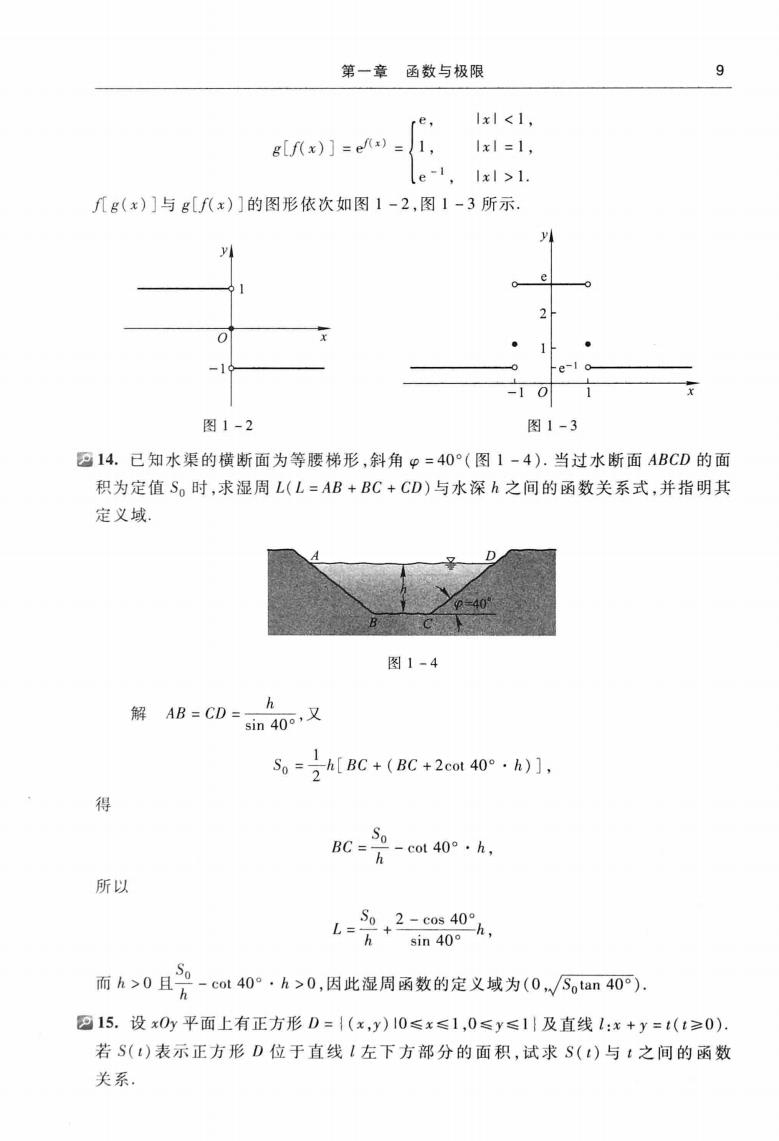
第一章函数与极限 9 re, 1xl<1. glf(x)]==1. 1x=1, e-,1xl>1. f几g(x)]与g[f(x)]的图形依次如图1-2,图1-3所示. 图1-2 图1-3 214.已知水渠的横断面为等腰梯形,斜角p=40°(图1-4).当过水断面ABCD的面 积为定值So时,求湿周L(L=AB+BC+CD)与水深h之间的函数关系式,并指明其 定义域 图1-4 h 解AB=CD=sn40,又 5=2h[BC+(BC+2co40.h)1, 得 所以 而A>0且产-m40A>0,因此混周两数的定义装为(0m0。 四15.设x0y平面上有正方形D={(x,y)10≤x≤1,0≤y≤1|及直线1:x+y=t(t≥0). 若S()表示正方形D位于直线1左下方部分的面积,试求S(:)与t之间的函数 关系