
例1.用对称式及参数式表示直线 x+y+z+1=0 2x-y+3z+4=0 解:先在直线上找一点, 令x=1,解方程组 -3=6,得y=0,:=-2 y+2=-2 故(1,0,-2)是直线上一点 再求直线的方向向量s 交已知直线的两平面的法向量为 n1=(1,1,1),n2=(2,-1,3) s1n1,31n2.s=m×n购
例1.用对称式及参数式表示直线 解:先在直线上找一点. 3 6 2 y z y z 再求直线的方向向量 令 x = 1, 解方程组 ,得 y 0 , z 2 交已知直线的两平面的法向量为 是直线上一点 . s . 1 2 s n ,s n 1 2 s n n

方 s=nxn2 三 111 =(4,-1,-3) 2-13 故所给直线的对称式方程为 x-l y z+2 二 4-1 -3 x=1+41 参数式方程为 = z=-2-31 解题思路:先找直线上一点: (1,0,-2) 再找直线的方向向量 是直线上一点
故所给直线的对称式方程为 参数式方程为 t 4 x 1 1 y 解题思路: 先找直线上一点; 再找直线的方向向量. (4, 1, 3) 1 2 s n n 2 1 3 1 1 1 i j k 是直线上一点

x-y+z=1, 设直线L的方程为 则的参数方程为(): 2x+y+z=4, x=1-2t, x=1-2t x=1-2t, x=1-2t, A. y=1+t, B.y=-1+t, C. y=1-t, D y=-1-t) z=1+3t z=1+3t z=1+3t z=1+3t
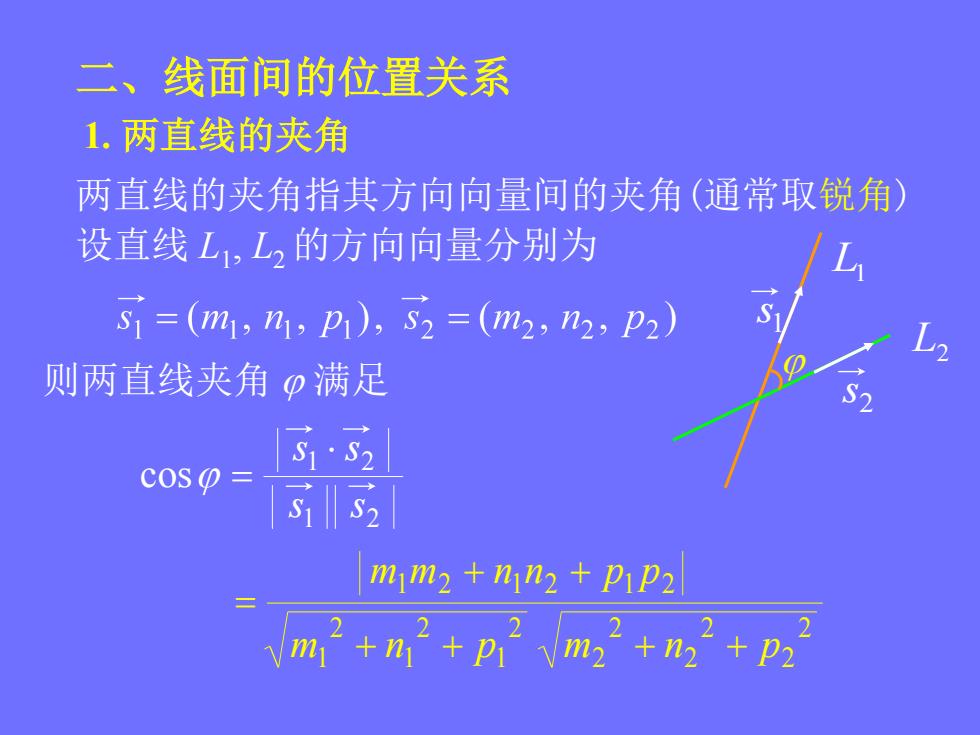
二、线面间的位置关系 1.两直线的夹角 两直线的夹角指其方向向量间的夹角(通常取锐角) 设直线L,L,的方向向量分别为 S1=(m1,h1,p1),S2=(m2,n2,P2) 则两直线夹角φ满足 cos 2 mim2+nn2+pip2 2 2 2 m1+n+p1vm2+n2+p2
L2 L1 二、线面间的位置关系 1. 两直线的夹角 则两直线夹角 满足 设直线 L1 , L2 的方向向量分别为 两直线的夹角指其方向向量间的夹角(通常取锐角) 1 2 1 2 1 2 m m n n p p 2 1 2 1 2 1 m n p 2 2 2 2 2 2 m n p 1 2 1 2 cos s s s s 1 s 2 s

特别有: (1)L⊥L2= 5112 =m1m2+n1n2+p1p2=0 (2)L111L2 5ll52 S 1=h1=P1 m2 n2 P2 s=(m1,n1,p) 32=(m2,n2,P2)
特别有: 1 2 (1) L L 1 2 (2) L // L 0 m1m2 n1n2 p1 p2 2 1 2 1 2 1 p p n n m m 1 2 s s 1 2 s //s L2 L1 1s 2s L2 L1 1s 2s